Zufallsexperiment / Zufallsversuch
Geschrieben von: Dennis RudolphMittwoch, 07. März 2018 um 20:59 Uhr
Was ein Zufallsexperiment bzw. ein Zufallsversuch, lernt ihr hier. Dies sehen wir uns an:
- Eine Erklärung, was man als Zufallsexperiment bezeichnet.
- Beispiele für Zufallsversuche (und was kein Zufallsexperiment ist).
- Aufgaben / Übungen damit ihr dies selbst üben könnt.
- Ein Video zu den Grundlagen der Wahrscheinlichkeitsrechnung.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Wir sehen uns gleich Grundlagen aus dem Bereich der Wahrscheinlichkeitsrechnung an. Viele Vorkenntnisse braucht ihr dazu nicht. Hilfreich ist es jedoch, wenn ihr ein bisschen mit Brüchen rechnen könnt. Wer damit Probleme hat sieht bitte in das Bruchrechnen rein.
Erklärung Zufallsexperiment
In der Mathematik versucht man in der Regel alles ganz genau auszurechnen. Die Fläche von einem Rechteck soll exakt berechnet werden oder die Geschwindigkeit eines Autos. Gerne lässt der Lehrer oder die Lehrerin etwas bis viele Stellen nach dem Komma berechnen. Aber nicht alles im Leben lässt sich exakt berechnen. Mehr noch: In vielen Fällen lässt sich eine genaue Vorhersage eines Ergebnisses gar nicht erreichen.
In diesen Fällen geht es darum zu berechnen, ob etwas eher eintreten kann oder vermutlich eher nicht. Man sagt dann, dass etwas wahrscheinlicher ist oder eher unwahrscheinlich. Ein wichtiger Begriff hierzu ist das Zufallsexperiment. Was versteht man darunter?
Eigenschaften Zufallsexperiment:
- Es gibt mehrere mögliche Ergebnisse.
- Das Experiment kann beliebig oft wiederholt werden.
- Zwei Ergebnisse können nicht gleichzeitig eintreten.
- Vor der Durchführung kann das Ergebnis nicht vorausgesagt werden.
- Die Regeln und Bedingungen werden während des Experiments nicht geändert.
Beispiele für Zufallsexperimente:
- Werfen einer Münze.
- Werfen eines Würfels.
- Drehen eines Glücksrades.
- Ziehen einer Karte (gemischter Stapel)
Kein Zufallsexperiment liegt hier vor:
- Messung der Gefriertemperatur von Wasser.
- Welches Datum welcher Wochentag ist.
- Welche Farben ein Regenbogen aufweist.
- Wie viele Seiten ein Buch hat.
Ein normaler Würfel hat 6 Seiten: Es kann damit 1, 2, 3, 4, 5 und 6 gewürfelt werden. Es gibt also 6 mögliche Ergebnisse. Die möglichen Ergebnisse kann man in einer Menge zusammenfassen, die man als Ergebnismenge bezeichnet. Interessiert man sich nur für ein Teil der Ergebnismenge - also beim Würfeln zum Beispiel nur die Zahlen 1, 2 und 3 - dann spricht man von einem Ereignis.
Anzeige:
Anzeigen:
Beispiele Zufallsversuche
In diesem Abschnitt nehmen wir uns einen Zufallsversuch und erklären mit diesem verschiedene Begriffe der Wahrscheinlichkeitsrechnung.
Beispiel 1: Münze werfen
Sehen wir uns einen Zufallsversuch bzw. ein Zufallsexperiment an. Dazu nehmen wir uns eine Münze. Werfen wir diese, kann dabei entweder Zahl oder Wappen rauskommen. Die nächste Grafik zeigt dies:
Manchmal wird eingewendet, dass die Münze auch auf der Seite landen kann. Dies kann jedoch nicht passieren, wenn die Münze nicht manipuliert ist und richtig geworden wird. Sie sollte sich dabei mehrfach in verschiedene Richtungen drehen.
Die Wahrscheinlichkeit Zahl zu werfen ist genauso groß wie die Wahrscheinlichkeit Wappen zu werfeln. Haben alle Ergebnisse die gleiche Wahrscheinlichkeit, spricht man von einem Laplace-Versuch oder Laplace-Experiment (Mehr dazu findet ihr unter Laplace-Versuch / Laplace-Experiment).
Es gibt zwei mögliche Ereignisse beim Werfen der Münze: Zahl und Wappen. Die Ergebnismenge wird mit Omega (Ω) bezeichnet und enthält diese beiden Ereignisse:
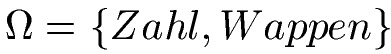
Die Wahrscheinlichkeit Zahl oder Wappen zu würfeln beträgt jeweils 1/2. Es gibt zwei Möglichkeiten wie der Wurf ausgehen kann (daher die 2 im Nenner) und eine der beiden Möglichkeiten wird durch Wappen und die andere durch Zahl dargestellt.
Einstufiger Zufallsversuch:
Wir werfen die Münze jetzt 1 Mal. Dies nennt man einen einstufigen Zufallsversuch. Wir werden dadurch entweder Zahl oder Wappen als Ergebnis bekommen. Die Wahrscheinlichkeit dafür ist jeweils 1/2. Wir kürzen dies im nächsten Diagramm mit Z für Zahl und W für Wappen ab.
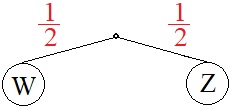
Mehrstufiger Zufallsversuch:
Wir hatten eben die Münze einmal geworfen und dies als einstufiges Zufallsexperiment bezeichnet. Natürlich können wir die Münze im Anschluss noch ein zweites Mal werfen. Damit sind wir beim zweistufigen Zufallsversuch (oder auch mehrstufiger Zufallsversuch).
Beim ersten Wurf hätten wir Wappen (W) werfen können. Im Anschluss können wir wieder Zahl (Z) oder Wappen (W) werfen. Daher zeichnen wir an das Wappen (W) erneut Zahl (Z) oder Wappen (W) an. Beim ersten Wurf hätte jedoch auch Zahl (Z) kommen können. Im Anschluss - also beim zweiten Mal werfen - können ebenfalls Zahl (Z) oder Wappen (W) geworfen werden. Daher zeichnen wir auch hier beides an.
Die Wahrscheinlichkeiten ändern sich nicht: Bei jedem weiteren Wurf ist die Wahrscheinlichkeit für Wappen wieder 1/2 und für Zahl ebenfalls wieder 1/2. Dies zeichnen wir in unser Baumdiagramm ein:
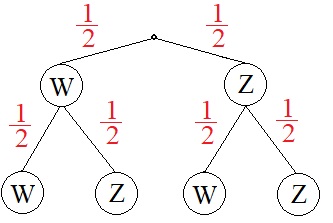
Aufgaben / Übungen Zufallsexperiment
Anzeigen:Video Zufallsversuche
Beispiele und Erklärungen
Im nächsten Video werden die Grundlagen der Wahrscheinlichkeitsrechnung besprochen. Dabei wird zunächst erklärt, was ein Zufallsversuch überhaupt ist und es werden Grundbegriffe der Wahrscheinlichkeitsrechnung besprochen. Im Anschluss geht es um einstufige und mehrstufige Zufallsversuche sowie das Baumdiagramm.
Nächstes Video »
Fragen mit Antworten Zufallsversuch
In diesem Abschnitt geht es um typische Fragen mit Antworten zu Zufallsexperimenten.
F: Wo finde ich schwierigere Aufgaben zu Zufallsversuchen und Baumdiagrammen?
A: Die weiter oben gezeigten Inhalte sind nur absolutes Grundwissen aus dem Bereich der Wahrscheinlichkeitsrechnung. Wir sehen uns weitere - auch schwerere Aufgaben - in den nächsten Artikeln an. Zu mehrstufigen Zufallsexperimenten mit schwierigeren Beispielen gibt es eigene Inhalte.
- Zufallsexperiment / Zufallsversuch
- Absolute / relative Häufigkeit
- Wahrscheinlichkeit
- Ereignis und Gegenereignis
- Laplace-Experiment / Laplace-Versuch
- Zweistufige / Mehrstufige Zufallsversuche
- Durchschnitt / Mittelwert berechnen
F: Wann wird das Thema Zufallsexperiment in der Schule behandelt?
A: Absolute Grundlagen der Wahrscheinlichkeitsrechnung werden oft schon in der Grundschule oder 5. Klasse besprochen. Eine Definition für Zufallsversuch oder andere Grundbegriffe der Wahrscheinlichkeitsrechnung folgen jedoch meistens erst ab der 6. Klasse oder 7. Klasse.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)

