Gleichnamige Brüche: Addition und Subtraktion
Geschrieben von: Dennis RudolphDonnerstag, 28. Dezember 2017 um 20:30 Uhr
Was gleichnamige Brüche sind und wie man diese addiert und subtrahiert, wird hier erklärt. Dies sehen wir uns an:
- Eine Erklärung, was ein gleichnamiger Bruch ist und wozu man diesen braucht.
- Viele Beispiele zum Rechnen mit gleichnamigen Brüchen.
- Aufgaben / Übungen zur Bruchrechnung.
- Videos zur Addition und Subtraktion von Brüchen.
- Ein Frage- und Antwortbereich zu diesem Gebiet.
Ein kleiner Tipp zum Start: Wenn ihr nicht wisst, was ein Bruch ist, werft bitte erst einmal einen Blick in den Hauptartikel Bruchrechnen. Ansonsten sehen wir uns nun gleichnamige Brüche an.
Erklärung gleichnamige Brüche
Eine kurze Erinnerung: Ein Bruch weist einen Zähler auf, einen Bruchstrich und einen Nenner. Der Zähler steht oben, der Nenner steht unten und dazwischen gibt es einen Bruchstrich.
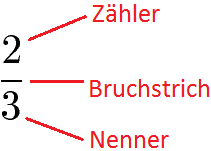
Haben zwei oder mehr Brüche den gleichen Nenner, dann bezeichnet man diese Brüche als gleichnamig. Gleichnamige Brüche werden benutzt um Brüche zu addieren, zu subtrahieren oder auch zu vergleichen.
Die folgenden Brüche sind gleichnamig, denn die Nenner sind gleich (in diesem Fall sind alle Nenner 3).
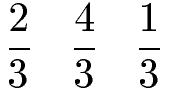
Die nächsten Brüche sind alle ungleichnamig, denn die Nenner sind alle verschieden.
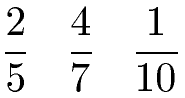
Um Brüche zu addieren, zu subtrahieren oder zu vergleichen bringt man diese auf einen gemeinsamen Nenner. Sind die Brüche von Beginn an gleichnamig, dann kann man direkt mit diesen arbeiten. Sind sie es nicht, sollte man diese zunächst gleichnamig machen. Wie dies geht lernt ihr unter ungleichnamige Brüche.
Anzeige:
Anzeigen:
Beispiele Addition, Subtraktion und Vergleich
In diesem Abschnitt findet ihr Beispiele zur Addition, Subtraktion und dem Vergleich von gleichnamigen Brüchen.
Beispiel 1:
Drei gleichnamige Brüche sollen addiert werden. Dies ist ganz einfach: Die Zähler werden addiert für das Ergebnis, der Nenner bleibt gleich.
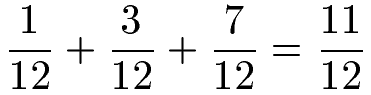
Beispiel 2:
In diesem Beispiel sollen drei gleichnamige Brüche subtrahiert werden. Auch hier muss nur im Zähler gerechnet werden. Der Nenner bleibt erhalten.
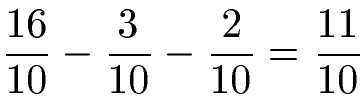
Beispiel 3:
Gleichnamige Brüche lassen sich ganz leicht vergleichen. Dazu muss man nur auf den Zähler achten. Ein Bruch ist kleiner, wenn der Zähler kleiner ist als bei einem anderen Bruch.
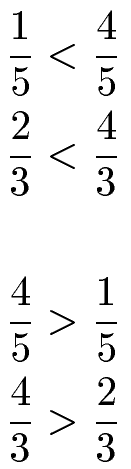
Aufgaben / Übungen Bruchrechnen
Anzeigen:Addition Brüche
Beispiele Additionsaufgaben
Die Addition sehen wir uns in diesem Video an. So werden einfache Additionen von Brüchen durchgeführt, wie zum Beispiel die Aufgabe 3/4 + 5/6 oder 1/3 + 5/15 und etliche weitere Übungen. Es wird auf Zähler und Nenner eingegangen, wie man einen gemeinsamen Nenner findet und was man unter dem Erweitern - dem Gegenteil vom Kürzen - versteht. Das Subtrahieren von Brüchen funktioniert ähnlich und wird ebenfalls behandelt. Dieses Video habe ich auf Youtube.com gefunden.
Nächstes Video »
Gleichnamige Brüche: Fragen mit Antworten
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zu diesem Thema an.
F: Wie kann man Brüche gleichnamig machen?
A: Die am einfachsten zu verstehende Methode besteht darin die beiden Nenner miteinander zu multiplizieren und dann die Brüche im Zähler jeweils anzupassen. Wie dies funktioniert seht ihr am einfachsten in Beispielen in den Artikeln Brüche addieren und Brüche subtrahieren sowie ungleichnamige Brüche. Eine andere Methode ist die Verwendung des kleinsten gemeinsamen Vielfachen.
F: Wann brauche ich keinen gleichnamigen Bruch?
A: Beim Brüche multiplizieren und Brüche dividieren können auch ungleichnamige Brüche verwendet werden.
Neue Artikel
- Fläche unter Kurve / Funktion Aufgaben und Übungen
- Fläche unter Kurve / Funktion berechnen
- Integral berechnen Aufgaben / Übungen
- Integral berechnen und Bedeutung
- Integrationsgrenzen Aufgaben / Übungen
- Integrationsgrenzen
- Bestimmtes Integral Aufgaben / Übungen
- Bestimmtes Integral berechnen / lösen
- Silben und Silbentrennung Aufgaben / Übungen
- Silben und Silbentrennung