Addition von Brüchen: Erklärung und Beispiele

Die Addition von Brüchen wird in diesem Artikel behandelt. Folgende Inhalte werden angeboten:

• Eine Erklärung, wie Brüche addiert werden.
• Beispiele zur Addition von Brüchen mit gleichen und verschiedenen Nennern.
• Aufgaben / Übungen mit denen ihr die Addition von Brüchen selbst üben könnt.
• Videos zum Addieren von Brüchen.
• Ein Frage- und Antwortbereich zur Addition von Brüchen.

Die Grundrechenarten Addition, Subtraktion, Multiplikation und Division gibt es auch für das Bruchrechnen. In der Bruchrechnung sind dabei drei Begriffe wichtig, die auch beim Addieren in den nächsten Abschnitten immer wieder auftauchen: Zähler, Bruchstrich und Nenner. Der Zähler steht über dem Bruchstrich, der Nenner unterhalb vom Bruchstrich.

Addition gleichnamiger Brüche

Bei gleichnamigen Brüchen sind die Nenner gleich. Die Addition gleichnamiger Brüche ist einfach: Addiere die Zähler und behalte den Nenner bei. Im nächsten Beispiel wird der Nenner 7 in die Summe übernommen.

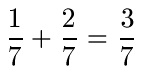
Bei der nächsten Aufgabe zu zwei gleichnamigen Brüchen ist der Nenner 11 und wird daher auch direkt in das Ergebnis übernommen. Im Zähler erhalten wir 2 + 3 = 5.

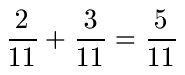
Ein unechter Bruch ist ein Bruch bei dem der Zähler mindestens so groß ist wie der Nenner. Bei der Addition von Brüchen kommt dies immer mal wieder vor. Im nächsten Beispiel ist der Zähler der Summe mit 4 größer als der Nenner mit 3.

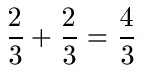
Bei der Addition von Brüchen entstehen manchmal Brüche, die gekürzt werden können. Einen Bruch zu kürzen bedeutet den Bruch im Zähler und im Nenner durch die gleiche Zahl zu teilen. Im nächsten Beispiel ergibt die Addition der Brüche 4 : 6. Beide Zahlen können durch 2 geteilt werden, um den Bruch auf 2 : 3 zu kürzen.

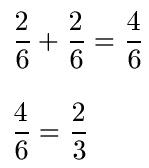
Die Addition von gleichnamigen Brüchen kann auch für mehrere Brüche eingesetzt werden. Sind alle Nenner gleich kann dieser Nenner in die Summe übernommen werden. Alle Zähler werden für das Ergebnis addiert.

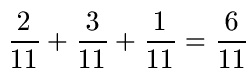
Im nächsten Beispiel werden drei Brüche addiert. Die 8 der drei Summanden wird in die Summe übernommen, die Zähler werden addiert. Das Ergebnis ist ein echter Bruch. Zur Erinnerung: Ein echter Bruch ist ein Bruch, bei dem der Zähler (hier 5) kleiner ist als der Nenner (hier 8).

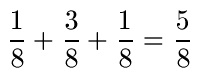
Die Addition gleichnamiger Brüche kann allgemein mit dieser Rechenregel beschrieben werden:

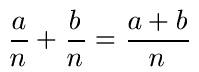
Anzeige:

Addition ungleichnamiger Brüche

Ungleichnamige Brüche sind Brüche mit unterschiedlichen Nennern. Bei der Addition von ungleichnamigen Brüchen kann kein Nenner direkt in das Ergebnis übernommen werden. Wir müssen mehrere Schritte durchführen um Brüche mit verschiedenen Nennern zu addieren.

Die am einfachsten zu verstehende Möglichkeit einen gemeinsamen Nenner zu finden besteht darin, alle Nenner miteinander zu multiplizieren. Die Addition ungleichnamiger Brüche durch Multiplikation der Nenner hilft insbesondere beim Rechnen mit kleineren Zahlen.

Ungleichnamige Nenner addieren Beispiel 1:

Zwei Brüche mit verschiedenen Nennern sollen addiert werden.

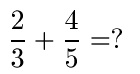
Mit 3 und 5 sind die Nenner verschieden. Um einen gemeinsamen Nenner tu finden, multiplizieren wir die beiden Nenner miteinander. Somit erhalten wir mit 3 · 5 = 15 einen Nenner, auf den wir beide Brüche bringen. Da dies auch der kleinstmögliche Nenner (kleinstes gemeinsames Vielfaches) ist, wird dieser Nenner auch als Hauptnenner bezeichnet.

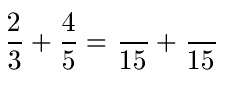
Für beide Zähler müssen die Zähler berechnet werden: Beim ersten Nenner haben wir mit 5 im Nenner multipliziert, um auf 15 zu kommen. Daher multiplizieren wir ebenfalls mit 5 im Zähler. Beim zweiten Nenner haben wir mit 3 im Nenner multipliziert, um auf 15 zu kommen. Daher auch die Multiplikation mit 3 im Zähler.

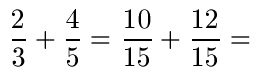
Werden Zähler und Nenner mit der gleichen Zahl multipliziert, wird dies in der Mathematik als Bruch erweitern bezeichnet. Das Erweitern der Brüche bringt uns zwei gleichnamige Brüche: Um die Summe zu berechnen addieren wir die Zähler und behalten den Nenner bei.

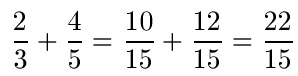
Einschub: Hauptnenner finden

Im letzten Beispiel wurde ein gemeinsamer Nenner durch Multiplikation der beiden Ausgangsnenner gefunden. Dabei kann auch ein relativ großer Nenner entstehen. Um den kleinstmöglichen Nenner zu finden (= Hauptnenner), ist es auch möglich, das kleinste gemeinsame Vielfache zu ermitteln. Das kleinste gemeinsame Vielfache - kurz kgV - lässt sich durch die Bestimmung der Vielfachen berechnen:

• 3: 3, 6, 9, 12, 15, 18, 21
• 5: 5, 10, 15, 20, 25
• Die 15 ist die kleinste gemeinsame Zahl, die bei beiden Vielfachen auftritt.

Werden die Zahlen größer kann zur Berechnung des kleinsten gemeinsame Vielfachen (kgV) die Primfaktorzerlegung verwendet werden.

Beispiel zur Addition ungleichnamiger Brüche

In diesem Abschnitt soll ein weiteres Beispiel zur Addition ungleichnamiger Brüche vorgerechnet werden. Berechnet werden soll 2/3 + 4/7. Wie lautet die Summe? Zunächst die komplette Berechnung, unterhalb werden die Rechenschritte noch einmal erläutert.

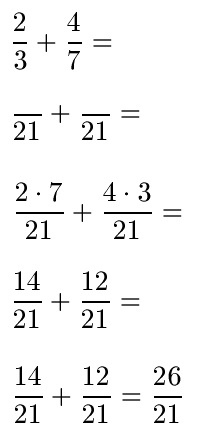
Die Addition der ungleichnamigen Brüche wurde in diesen Schritten berechnet:

• Wir multiplizieren die beiden Nenner: 3 · 7 = 21.
• Um den ersten Bruch auf 21 im Nenner zu bringen muss mit 7 multipliziert werden.
  • Der Zähler des ersten Bruchs wird mit 7 multipliziert.
• Um den zweiten Bruch auf 21 im Nenner zu bringen muss mit 3 multipliziert werden.
  • Der Zähler des zweiten Bruchs wird ebenfalls mit 3 multipliziert.
• Die nun gleichnamigen Brüche werden addiert.

Anzeigen:

Aufgabe / Übungen Addition Brüche

Aufgabe 1: In diesem Abschnitt bekommt ihr Rechenaufgaben und Fragen zum Addieren von Brüchen. Wer eine Frage oder Aufgabe nicht mag, der kann auch auf "Überspringen" klicken. Zur ersten Frage: Wie lautet das Ergebnis von 1/3 + 1/3?

• 3/3
• 4/3
• 1/3
• 2/3

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Addition von Brüchen Videos

Fragen und Antworten: Addition Brüche