Kommutativgesetz Erklärung und Beispiele

Das Kommutativgesetz sehen wir uns hier an. Dies bekommt ihr:

• Eine Erklärung und Formeln, was das Kommutativgesetz besagt.
• Viele Beispiele zum Kommutativgesetz.
• Aufgaben / Übungen zu diesem Rechengesetz.
• Videos zum Kommutativgesetz mit Erklärungen.
• Ein Frage- und Antwortbereich rund um dieses Thema.

Wir sehen uns gleich das Kommutativgesetz an. Wer hier Verständnisprobleme bekommen sollte, dem helfen vielleicht noch die Artikel zu den Grundrechenarten: Dies sind Addition, Subtraktion, Multiplikation und Division.

Erklärung Kommutativgesetz

Starten wir mit einer Erklärung. Das Kommutativgesetz ist eine Regel der Mathematik. Im Deutschen wird diese Rechenregel auch Vertauschungsgesetz genannt. Eine Definition:

Das Kommutativgesetz wird mit zwei Formeln / Gleichungen für reelle Zahlen dargestellt.

Kommutativgesetz der Addition:

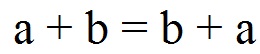
Kommutativgesetz der Multiplikation:

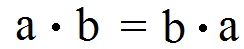
Eigentlich also ganz einfach. Dennoch sehen wir uns dies mit einigen Zahlen einmal an.

• 5 + 3 = 3 + 5
• 5 + 3 = 8
• 3 + 5 = 8

• 4 · 2 = 2 · 4
• 4 · 2 = 8
• 2 · 4 = 8

Das Kommutativgesetz gilt nicht für die Subtraktion und das Kommutativgesetz gilt auch nicht für die Division. Zur Verdeutlichung auch hier ein paar Zahlen:

• 5 - 2 = 2 - 5 falsch
• 5 - 2 = 3
• 2 - 5 = -3

• 8 : 2 = 2 : 8 falsch
• 8 : 2 = 4
• 2 : 8 = 0,25

Kommutativgesetz Vektoren:

Das Kommutativgesetz gilt auch bei der Addition von Vektoren. Wer Vektoren noch nicht kennt: Mit Vektoren beschreibt man Richtungen. Auch hier ein Beispiel: Ob ich erst 2 Meter nach oben und dann 3 Meter nacht rechts gehe oder ob ich erst 3 Meter nach rechts gehe und danach 2 Meter nach oben macht keinen Unterschied. Ich lande stets an der gleichen Stelle.

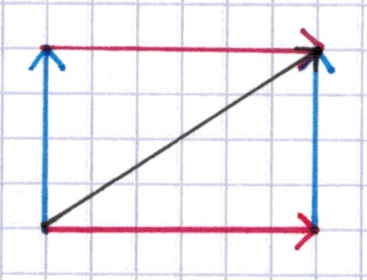
Im nächsten Abschnitt sehen wir uns weitere Beispiele zum Kommutativgesetz an.

Anzeige:

Beispiele Kommutativgesetz

In diesem Abschnitt sehen wir uns eine Reihe an Beispielen zum Kommutativgesetz an.

Beispiel 1:

Es folgen eine Reihe an Aufgaben. Sage, ob für die Aufgabe das Kommutativgesetz gilt und berechne die Lösung.

• 16 : 8 =
• 9 · 3 =
• 7 - 4 =
• 8 + 3 =

Lösung:

• 16 : 8 = 2 ist nicht kommutativ.
• 9 · 3 = 27 ist kommutativ.
• 7 - 4 = 3 ist nicht kommutativ.
• 8 + 3 = 11 ist kommutativ.

Beispiel 2:

Zeige mit dem Zahlenstrahl, dass 3 + 4 = 7 kommutativ ist.

Lösung:

Wir zeichnen 3 + 4 und 4 + 3 jeweils auf einen Zahlenstrahl ein. Wie man sehen kann, landen wir in beiden Fällen auf der 7.

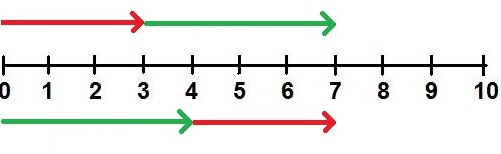
Beispiel 3:

Das Kommutativgesetz soll nun für eine Flächenberechnung gezeigt werden. Eine Tafel Schokolade soll 20 Zentimeter lang und 10 Zentimeter breit sein. Berechne die Fläche der Tafel!

Lösung:

Diese Tafel Schokolade ist ein Rechteck. Man berechnet die Fläche, indem man die Länge mit der Breite multipliziert. Ob man jedoch Länge mal Breite oder Breite mal Länge rechnet ändert an der Fläche der Tafel Schokolade nichts.

Beispiel 4:

Brüche stellen Anteile an etwas ganzem dar. Nehmen wir an, wir teilen eine Pizza in 4 gleichgroße Stücke. Davon nehmen wir erst einmal ein Stück Pizza und dann 2 weitere Stücke Pizza. Wie viel der Pizza wurde nun genommen. Spielt die Reihenfolge dabei eine Rolle?

Lösung:

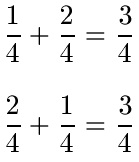
Ob ich erst 1 Stück nehme und dann 2 Stücke oder erst 2 Stücke und danach 1 Stück spielt keine Rolle. Am Ende sind es stets 3 von 4 Stücken.

Aufgaben / Übungen Kommutativgesetz

Aufgabe 1: Was ergibt 5 + 3?

• 8
• 10
• 7
• 9

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 7 Aufgaben erfolgreich gelöst.

Anzeigen:

Kommutativgesetz Video

Kommutativgesetz Fragen mit Antworten