Additionsverfahren (Subtraktionsverfahren) bei Gleichungssystemen

Wie man lineare Gleichungssysteme mit dem Additionsverfahren (Subtraktionsverfahren) löst, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung wie Additionsverfahren bzw. Subtraktionsverfahren funktionieren.
• Beispiele wie man damit Gleichungssysteme löst.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zu linearen Gleichungssystemen.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es gibt verschiedene Möglichkeiten lineare Gleichungssysteme zu lösen. Wir sehen uns hier das Additionsverfahren bzw. Subtraktionsverfahren an. Weitere Verfahren findet ihr im Hauptartikel lineare Gleichungssysteme lösen.

Erklärung Additionsverfahren / Subtraktionsverfahren

In der Mathematik kommt es vor, dass man mehrere Gleichungen mit mehreren Unbekannten (Variablen) hat. Diese sollen im Anschluss gemeinsam gelöst werden. Ziel ist es, für jede Variable eine Zahl zu finden, die alle Gleichungen korrekt löst.

Die Idee beim Additionsverfahren (Subtraktionsverfahren) ist, dass man zwei oder drei Gleichungen so umformt, dass man durch Addition oder Subtraktion eine Variable verschwinden lassen kann. Klingt kompliziert, ist meistens jedoch recht einfach. Die nächsten Beispiele zeigen dies für lineare Gleichungssysteme mit 2 oder 3 Gleichungen bzw. 2 oder 3 Variablen.

Beispiel 1: Additionsverfahren mit 2 Variablen bei 2 Gleichungen

Wir haben ein lineares Gleichungssystem mit zwei Gleichungen und zwei Variablen (x und y). Dieses soll mit dem Additionsverfahren gelöst werden. Wie groß sind x und y?

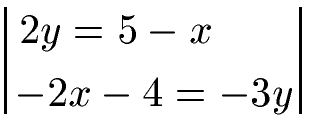
Lösung:

Zunächst sortieren wir beide Gleichungen um. Wir schaffen alle Terme mit Variablen auf die linke Seite der Gleichung und die reinen Zahlen auf die rechte Seite. Dies machen wir auch so, dass die Terme mit x untereinander stehen und die Terme mit y untereinander stehen.

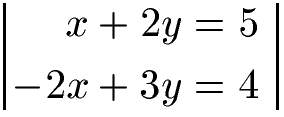
Als nächstes multiplizieren wir die erste Gleichung mit 2.

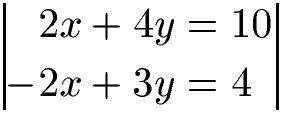
Wir haben jetzt zwei Gleichungen. In der ersten Gleichung haben wir 2x vorne und in der zweiten Gleichung -2x. Würden wir jetzt dies addieren fliegt die Variable x raus. Wir haben 2x + (- 2x) = 0 vorne. Danach 4y + 3y = 7y und 10 + 4 = 14. Wir erhalten 7y = 14 und damit y = 2.

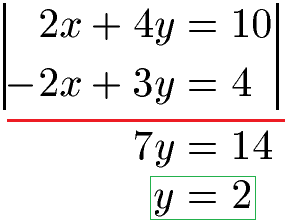
Wir wissen nun, dass y = 2 ist. Damit wollen wir noch x ausrechnen. Daher nehmen wir von weiter oben eine Gleichung und setzen y hier ein.

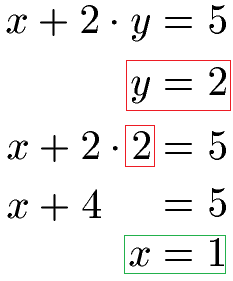
Wir berechnen damit x = 1und y = 2 als Lösung für beide Gleichungen des (linearen) Gleichungssystems.

Anzeige:

Beispiele Additionsverfahren / Subtraktionsverfahren

In diesem Bereich sehen wir uns noch das Additionsverfahren bzw. Subtraktionsverfahren für 3 Gleichungen mit 3 Unbekannten an.

Beispiel 2: 3 Gleichungen mit 3 Unbekannten

Wir haben ein lineares Gleichungssystem mit 3 Gleichungen und 3 Variablen. Diese Variablen sind x, y und z. Wie groß sind diese drei Unbekannten?

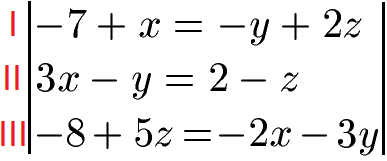
Lösung:

Zunächst sortieren wir das Gleichungssystem. Wir schaffen alle Terme mit x, y und z auf die linke Seite und die Zahlen ohne Variablen nach rechts. Dabei sollen x, y und z jeder Gleichung untereinander stehen.

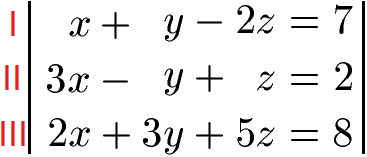
Um mit dem Additionsverfahren bzw. Subtraktionsverfahren das Gleichungssystem zu lösen, nehmen wir uns zwei Gleichungen heraus. Wir wollen dabei zunächst x beseitigen. Wir nehmen die Gleichung (I) und die Gleichung (II) zu Beginn.

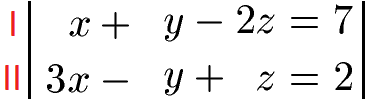
Die obere Gleichung (I) multiplizieren wir mit 3.

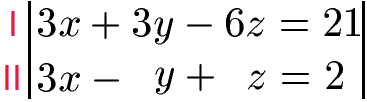
Wir können nun die beiden Gleichungen subtrahieren (Subtraktionsverfahren) wodurch die Variable x rausfliegt. Wir erhalten vorne 3x - 3x = 0. Außerdem erhalten wir 3y - (-y) = 4y und -6z - z = -7z. Auf der rechten Seite 21 - 2 = 19.

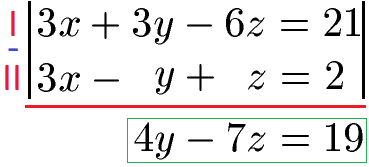
Wir haben mit Hilfe der ersten und zweiten Gleichung nun x rausgeworfen. Das x müssen wir jetzt noch aus der dritten Gleichung entfernen. Dies machen wir, indem wir die dritte Gleichung (III) nehmen und eine der beiden anderen Gleichungen. Wir nehmen hier einfach noch die erste Gleichung (I).

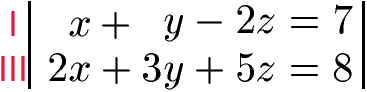
Die oberste Gleichung multiplizieren wir mit 2.

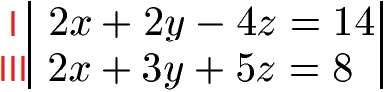
Durch Subtraktion der beiden Gleichungen können wir auch hier x entfernen. Vorne erhalten wir 2x - 2x = 0. Danach 2y - 3y = -y und -4z -5z = -9z. Auf der rechten Seite der Gleichung 14 - 8 = 6.

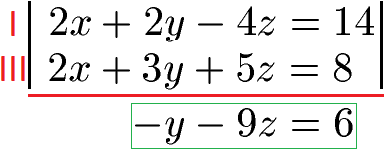
Wir haben aus dem linearen Gleichungssystem mit 3 Gleichungen und 3 Unbekannten jetzt ein lineares Gleichungssystem mit 2 Gleichungen und 2 Unbekannten gemacht. Diese beiden Gleichungen sind in grün markiert.

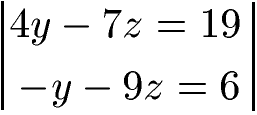
Wir multiplizieren die untere Gleichung mit 4 und addieren. Dadurch fliegt y raus. Außerdem erhalten wir -7z + (-36z) = -43z. Rechts erhalten wir 19 + 24 = 43.

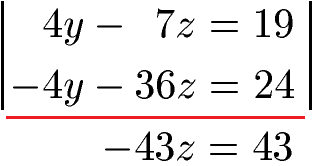
Wir rechen damit z = -1 aus.

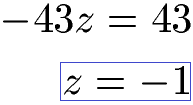
Wir kennen nun z und setzen dies in eine Gleichung mit y und z ein. Wir nehmen dafür zum Beispiel 4y - 7z = 19 und setzen z = -1 ein. Damit berechnen wir y = 3.

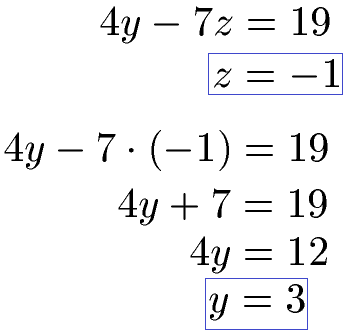
Wir setzen als letztes y und z in eine der Startgleichungen ein und berechnen x.

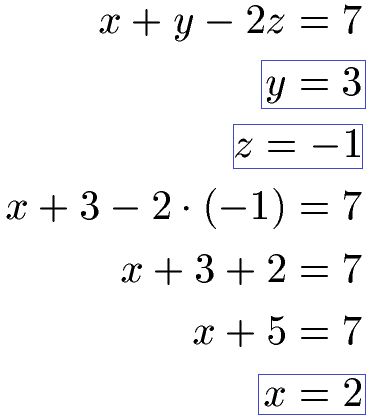
Wir erhalten als Lösung x = 2, y = 3 und z = -1. Wer mag kann noch die Lösungsmenge wie folgt angeben:

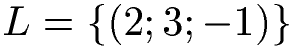
Aufgaben / Übungen Gleichungssysteme

Aufgabe 1: Wie groß sind x und y im nächsten Gleichungssystem?

• x = 4 und y = 2
• x = 3 und y = 3
• x = 2 und y = 4
• x = 1 und y = 5

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 7 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Gleichungssysteme

Fragen mit Antworten Additionsverfahren