Rechteck Fläche / Flächeninhalt

Wie man die Fläche von einem Rechteck berechnet, lernst du hier. Dies sehen wir uns an:

• Eine Erklärung mit Formel zur Fläche von einem Rechteck.
• Viele Beispiele mit Zahlen und Einheiten zum Flächeninhalt eines Rechtecks.
• Aufgaben / Übungen damit ihr alles selbst üben könnt.
• Ein Video zu diesem Thema.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Hinweis: Beim Berechnen der Fläche eines Rechtecks tauchen gleich Variablen (Buchstaben) auf. Diese sind ein Platzhalter für eine Zahl. Wer dazu erst noch mehr lesen möchte, kann gerne noch in Was ist eine Variable? reinsehen.

Ein Rechteck hat eine Länge und eine Breite. Diese setzt man in Meter, Zentimeter oder einer anderen Längeneinheit ein. Wer davon noch keine Ahnung hat, sollte noch in die Längeneinheiten einen Blick werfen.

Fläche Rechteck Formeln

Ein Rechteck hat vier Ecken und vier rechte Winkel. Die gegenüberliegenden Seiten sind gleich lang und werden meistens mit "a" und "b" bezeichnet. Mit den Seitenlängen "a" und "b" wird definiert, wie groß der Flächeninhalt des Rechtecks ist.

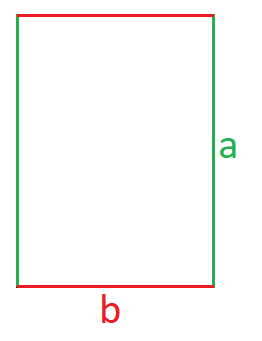
Wichtig: Es spielt für die Größe der Fläche von einem Rechteck keine Rolle, welche Länge oder Breite als "a" und welche als "b" bezeichnet wird.

Formel Rechteck Fläche:

Der Flächeninhalt "A" kann berechnet werden, indem die Länge des Rechtecks mit der Breite multipliziert wird.

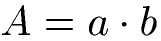
Soll mit dem Flächeninhalt "A" die Seitenlänge "a" berechnet werden, kann die Gleichung nach "a" umgestellt werden. Zur Berechnung der Seite a ist es jedoch nötig die Seitenlänge b zu kennen.

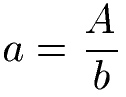
Soll mit der Fläche "A" die Seitenlänge "b" berechnet werden, kann die Gleichung nach "b" umgestellt werden. Zur Berechnung der Seite b ist es jedoch nötig die Seitenlänge a zu kennen.

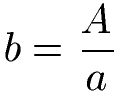
Der Flächeninhalt kann alternativ auch mit dem Umfang des Rechtecks berechnet werden. Kennst du den Umfang "U" und die Seitenlänge "a" kann die Fläche mit der folgenden Formel berechnet werden.

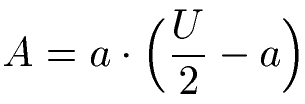
Die Fläche kann ebenfalls berechnet werden wenn der Umfang "U" und die Seitenlänge "b" bekannt ist. Die Gleichung für die Flächenberechnung lautet dann wie folgt.

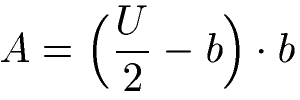
Im nächsten Abschnitt sehen wir uns Beispiele zur Berechnung der Fläche an.

Anzeige:

Beispiele Flächeneinhalt Rechteck

In diesem Abschnitt sollen einige Beispiele zum Flächeneinhalt von einem Rechteck vorgerechnet werden.

Beispiel 1:

Ein rechteckiges Stück Papier sei 30 cm lang und 20 cm breit. Wie groß ist die Fläche des Papiers?

Lösung:

Sowohl die Länge, als auch die Breite sind in Zentimeter angegeben. Aus diesem Grund können wir die beiden Angaben direkt multiplizieren, um die Fläche zu erhalten. Wir multiplizieren dazu 20 mit 30 und erhalten 600. Und Zentimeter mal Zentimeter ergibt Quadratzentimeter (cm · cm = cm²).

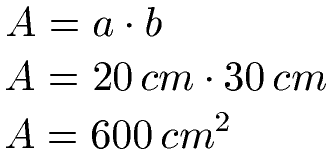
Beispiel 2:

Ein Grundstück hat die Form eines Rechtecks. Das Grundstück ist 32,15 Meter breit und 48,82 Meter lang. Wie groß ist das Grundstück?

Lösung:

Beide Angaben liegen als Meter vor. Daher können wir direkt multiplizieren. Wer bei den Zahlen keinen Taschenrechner einsetzen darf oder will, kann dies mit Hilfe der schriftlichen Multiplikation mit Komma lösen. Rechnet man, erhält man 32,15 · 48,82 = 1569,563. Meter mal Meter ergibt Quadratmeter (m · m = m²).

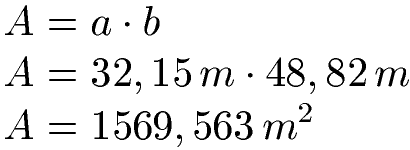
Beispiel 3:

Ein Schüler bekommt eine Textaufgabe: Ein Haus hat die Grundfläche eines Rechtecks. Es sei 12 Meter breit und 1200 Zentimeter lang. Wie groß ist die Fläche? Dem Lehrer hat der Schüler folgende Rechnung hingelegt. Wo ist der Fehler? Wie lautet das richtige Ergebnis?

Lösung:

Hier wurden die Einheiten Meter und Zentimeter vermischt. Dies darf man nicht. Daher rechnen wir für das richtige Ergebnis zunächst die 1200 cm in 12 Meter um. Wer zum Umrechnen noch mehr lernen möchte, sieht in Längeneinheiten umrechnen / umwandeln. Wir setzen nun die bisherigen 12 Meter und die umgerechneten 12 Meter ein und rechnen 144 Quadratmeter aus.

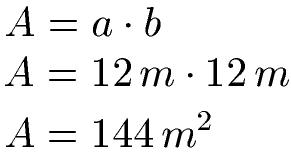
Hinweis: Wie sich durch die Berechnung zeigt ist die Fläche eigentlich ein Quadrat und kein Rechteck.

Beispiel 4:

Ein Raum weist eine Fläche von 21 Quadratmeter auf. Der Raum ist 873 Zentimeter lang. Wie Breit ist der Raum?

Lösung:

Die Fläche ist in Quadratmeter angegeben. Daher wandeln wir die 873 Zentimeter zunächst in Meter um. Dies sind 8,73 Meter. Wir setzen dies für a in die Formel ein. Um nun b zu berechnen, müssen wir die 21 Quadratmeter der Fläche durch die 8,73 Meter teilen. Wer hier noch mehr erfahren möchte, der sieht in Gleichung auflösen / umstellen noch rein. Dabei kürzt sich das Meter einmal raus.

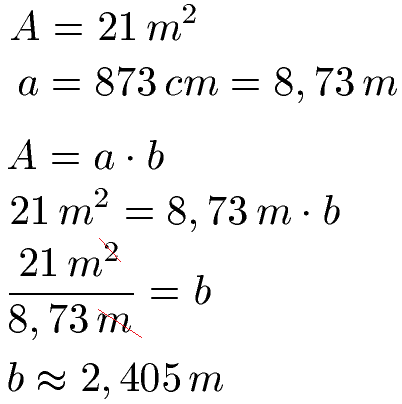
Übungen / Aufgaben Rechteck Fläche

Aufgabe 1: Bevor wir rechnen eine kurze Frage zum Aufwärmen. Mit welcher Formel berechnet man die Fläche von einem Rechteck?

• A = a * b
• A = 2a * b
• U = 2a + 2b
• U = a + b

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Fläche Rechteck

Fragen mit Antworten zu Rechteck Flächeninhalt