Wurzelfunktion: Beispiel und Definitionsbereich
Geschrieben von: Dennis RudolphMittwoch, 19. Dezember 2018 um 17:52 Uhr
Was man unter einer Wurzelfunktion versteht und wie man damit umgeht, lernt ihr hier. Folgende Inhalte werden angeboten:
- Eine Erklärung, was eine Wurzelfunktion ist.
- Beispiele und Definition einer Wurzelfunktion.
- Übungen zu diesem Thema.
- Ein Video zum Umgang mit Wurzeln.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Wir sehen uns hier gleich Wurzelfunktionen an. Hilfreich beim Verständnis ist es, wenn ihr bereits bei einfachen Zahlen / Variablen die Wurzel ziehen könnt. Es hilft auch wenn ihr wisst was eine Funktion ist. Wer davon noch keine Ahnung hat sieht bitte in diese Inhalte rein.
Wurzelfunktion: Beispiel und Definition
Sehen wir uns zunächst einmal eine Definition für eine Wurzelfunktion an:
Eine Wurzelfunktion hat diese Form:
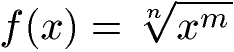
Die Wurzel darf nicht negativ werden. Der Wurzelexponent (n) muss 2 oder größer sein, sprich Quadratwurzel, Kubikwurzel etc.
Einige Beispiele für Wurzelfunktionen:
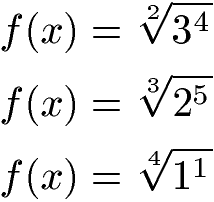
Fasst man den Wurzelbegriff für Wurzelfunktionen etwas weiter kann man auch diese Gleichungen als Wurzelfunktion bezeichnen:
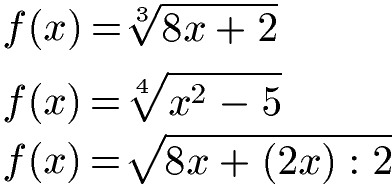
Anzeige:
Anzeigen:
Wurzelfunktion und Gleichungen
Wie kann man so eine Wurzelfunktion bzw. eine Wurzelgleichung lösen? Sehen wir uns dazu ein Beispiel an.
Beispiel 1: Wurzelfunktion / Wurzelgleichung lösen
Bestimme die Definitionsmenge und die Lösungsmenge für die folgende Gleichung,
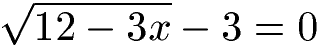
Lösung:
Unter einer Wurzel darf keine negative Zahl entstehen. Daher muss mindestens eine Null oder größer entstehen. Dies ist der Fall wenn x maximal 4 groß ist. Dies schreiben wir in die Definitionsmenge:
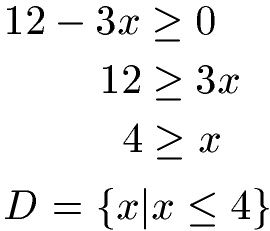
Für die Berechnung der Lösung isolieren wir zunächst die Wurzel und quadrieren beide Seiten der Gleichung. Wir lösen nach x auf und erhalten x = 1.
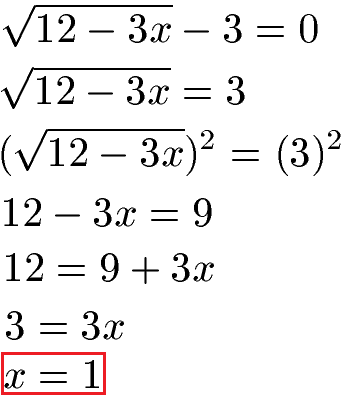
Löst x = 1 wirklich unsere Gleichung? Wir testen dies mit einer Probe. Wir setzen x = 1 und sehen nach, ob die Gleichung korrekt ist. Dies ist der Fall, daher kommt x = 1 in die Lösungsmenge.
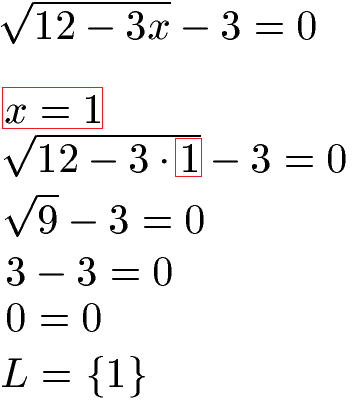
Aufgaben / Übungen Wurzelfunktion
Anzeigen:Video Wurzelfunktion / Gleichung
Beispiele und Erklärungen
In diesem Video wird die Wurzelfunktion bzw. Gleichung behandelt. Dies sehen wir uns an:
- Was ist eine Wurzelfunktion bzw. Wurzelgleichung?
- Wie löst man solch eine Gleichungsart?
- Wie berechne ich die Definitionsmenge und Lösungsmenge?
- Wie führe ich eine Probe durch?
Nächstes Video »
Fragen mit Antworten Wurzelfunktion
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zu Wurzelfunktionen an.
F: Gibt es auch Gleichungen mit Wurzeln bei denen man mehrfach quadrieren muss?
A: Gibt es, ja. Nach dem ersten Quadrieren der Gleichung existiert im Anschluss noch immer eine Wurzel. Nach dieser muss die Gleichung aufgelöst werden und danach muss erneut ein Quadrieren durchgeführt werden. Beachtet danach, dass ihr wieder eine Probe durchführen müsst.
F: Was sollte man noch zu diesen Funktionen wissen?
Funktionen / Gleichungen mit Wurzeln können auch etwas schwieriger werden. Ihr solltet daher noch die Bruchrechnung und die Binomischen Gleichungen beherrschen. Jedoch werden solche Arten etwas seltener behandelt und sind daher nicht Teil dieses Artikels hier.
F: Welche Inhalte sollte ich mir noch ansehen?
A: Werft noch einen Blick auf diese Gebiete:
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
