Zehnerpotenzen Präfixe / Vorsilben

Die Präfixe (Vorsilben) von Zehnerpotenzen behandeln wir hier. Dies gibt es:

• Zwei Tabellen zu Zehnerpotenzen für kleine Zahlen und große Zahlen mit Präfixen (Vorsilben).
• Beispiele zum Rechnen mit Zehnerpotenzen.
• Aufgaben / Übungen damit ihr dieses Thema selbst üben könnt.
• Ein Video zum Umgang mit Zehnerpotenzen.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Zehnerpotenzen mit Präfixe und Tabelle

Möchte man sehr große oder sehr kleine Zahlen darstellen, dann nutzt man dafür sehr häufig eine Potenzschreibweise mit der 10 als Basis. Wem das Wort Basis nichts sagt oder wer gar keine Ahnung von Potenzen hat, sieht bitte in den Artikel Potenzen rechnen rein.

Beginnen wir mit ganz kleinen Zahlen. Diese beinhalten ein Minuszeichen im Exponenten. Die nächste Tabelle beinhaltet auf der linken Seite die Dezimalzahl (Kommazahl). Gerade wenn hier sehr viele Nullen hinter dem Komma auftauchen wird es sehr schwer zu sehen, um welche Zahl es sich handelt. Daher kann man diese Zahl entweder in Form einer Potenz schreiben oder man verwendet ein Präfix mit einem entsprechenden Zeichen (Abkürzung).

Bild 1: Tabelle mit Zehnerpotenzen und Präfix für kleine Zahlen

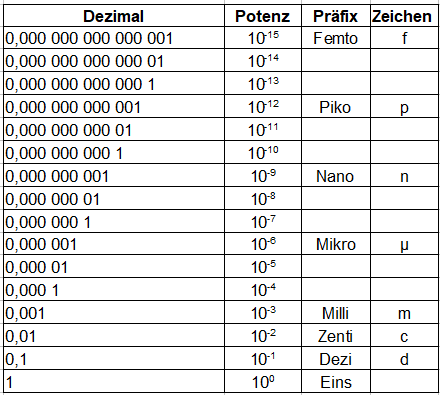
Als Präfix - auch Vorsatz oder Vorsilbe von einigen genannt - gibt es typischerweise Dezi, Zenti, Milli, Mikro, Nano, Piko oder auch Femto. Da dies oft zu lange ist, kürzt man ein Präfix oft mit einem einzigen Buchstaben (Zeichen oder auch Abkürzung) genannt ab. Sehen wir uns ein Beispiel zum besseren Verständnis an.

Beispiel:

Eine Strecke von 0,000 000 001 Metern ist sehr unübersichtlich. Um diese Zahl abzukürzen, kann man diese Länge auch mit 10^-9 Metern als Potenz angeben. Dies entspricht auch 1 Nanometer, abgekürzt 1 nm.

Auch ganz große Zahlen kann man mit einer Zehnerpotenz darstellen. Auch hier sollte man verschiedene Präfixe (Vorsilben) kennen, wie zum Beispiel Deka, Hekto, Kilo, Mega, Giga, Tera, Peta und Exa. Die nächste Tabelle zeigt euch dabei die Dezimalzahl, danach die Potenz, dann den Namen - also den Präfix - und im Anschluss das Kürzel dafür.

Bild 2: Tabelle mit Zehnerpotenzen und Präfix für große Zahlen

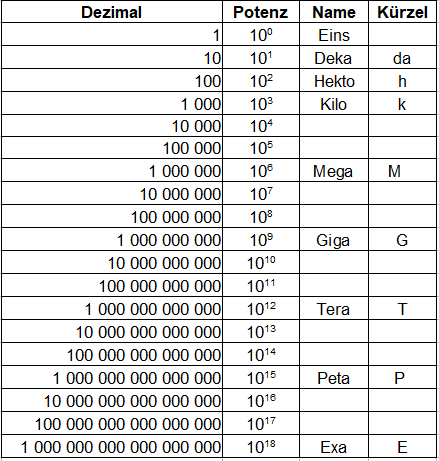
Beispiel: Nehmen wir an, dass wir eine Länge von einer Million Metern haben. Dies sind 1 000 000 Meter. Man kann dies aber auch viel kürzer schreiben mit 10⁶ Meter, kurz 10⁶ m. Alternativ ist es auch 1 Megameter, kurz 1 Mm.

Anzeige:

Beispiele Präfixe bei Zehnerpotenzen

In diesem Abschnitt sollen zum Umgang mit Präfixen bei Zehnerpotenzen einige Beispiele vorgerechnet werden.

Beispiel 1:

Gegeben sei eine Zahl mit Präfix. Rechne die Zahl 10^-3 in eine Dezimalzahl um.

Lösung:

Die Gleichung um eine Zehnerpotenz mit negativem Exponenten in eine Dezimalzahl umzuwandeln sieht so aus:

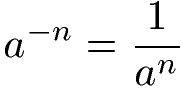
Setzen wir unsere 10 als Basis ein und die -3 als Exponent. Die Rechnung sieht damit so aus:

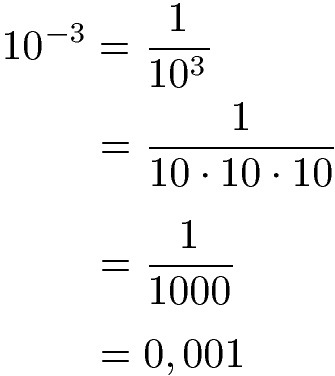
Beispiel 2: Eine kleine Strecke ist 34,6 nm lang. Rechne diese Länge in Meter um.

Lösung:

Es gibt mehrere Möglichkeiten diese Angabe umzurechnen.

Möglichkeit 1: Wir wissen aus der Tabelle von weiter oben, dass 1 nm = 0,000 000 001 m sind. Damit sind 34 nm 0,000 000 034 m. Hängen wir noch die 6 dahinter werden aus 34,6 nm = 0,000 000 0346 m.

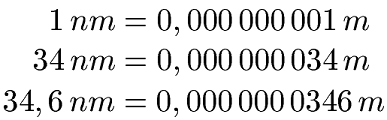
Möglichkeit 2:

Aus der Tabelle wissen wir, dass 1 nm = 10^-9 m ist. Daher können wir die Länge aus der Aufgabenstellung schreiben als 34,6 · 10^-9 m. Mit der Gleichung

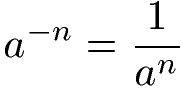
von weiter oben kommt man damit auf:

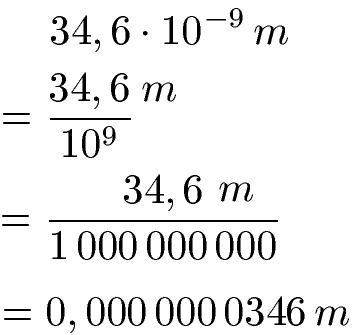
Beispiel 3:

Die Zahl 0,000 081 2 m soll in Mikrometer angegeben werden. Wie lautet das Ergebnis?

Lösung:

Aus der Tabelle wissen wir, dass 0,000 001 m = 1 µm sind. Wenn man sich dies untereinander schreibt, sieht man, dass dies 81,2 µm sind.

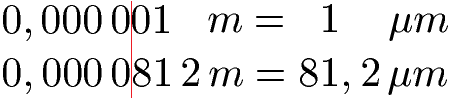
Übungen / Aufgaben Zehnerpotenzen

Aufgabe 1: Rechnet 10² aus. Was kommt dabei heraus?

• 10
• 1000
• 10000
• 100

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 8 Aufgaben erfolgreich gelöst.

Anzeigen:

Videos Zehnerpotenzen

Fragen und Antworten Präfix Zehnerpotenzen