Grundwert berechnen: Formel, Beispiele und Definition

Was der Grundwert in der Prozentrechnung ist, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was der Grundwert ist und wie man diesen berechnet.
• Viele Beispiele zum Umgang und Formel beim Grundwert.
• Aufgaben / Übungen um dieses Thema selbst zu üben.
• Ein Video zur Prozentrechnung.
• Ein Frage- und Antwortbereich zu diesem Thema.

Hinweis: Wir legen den Schwerpunkt hier auf den Grundwert beim Prozentrechnen. Solltet ihr das Thema allgemein brauchen, dann werft doch noch einen Blick auf den Hauptartikel Prozentrechnung.

Grundwert Erklärung und Definition

Klären wir zunächst, was der Grundwert ist.

Definition:

Wem es noch nicht klar ist: Ein Prozent (1%) ist nicht anderes als 1 : 100. Dies wird hoffentlich bei den Beispielen weiter unten noch klar (seht also rein).

Formel Grundwert berechnen:

Es gibt typischerweise zwei Formeln, um den Grundwert zu berechnen. Diese lauten:

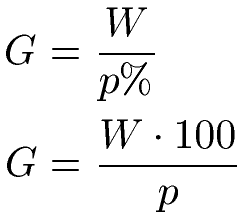
Dabei steht:

• G für den Grundwert
• p % heißt der Prozentsatz
• p ist die Prozentzahl (auch Prozentfuß genannt)
• W ist der Prozentwert

Die Formeln lauten damit in Worten:

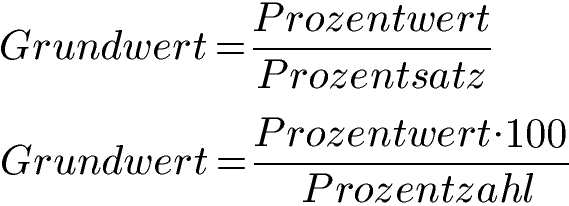
Manchmal wird in Formeln der Prozentrechnung auch der Prozentwert mit PW und der Grundwert mit GW abgekürzt. Alternativ kann man den Grundwert auch mit dem Dreisatz berechnen. Wie man Formeln und Dreisatz anwendet, sehen wir uns gleich mit Beispielen an.

Anzeige:

Grundwert Beispiele

In diesem Abschnitt sehen wir uns Beispiele zum Berechnen vom Grundwert an. Um den Grundwert zu berechnen müssen Prozentwert und Prozentsatz bzw. Prozentwert und Prozentzahl vorliegen.

Beispiel 1:

Herr Meyer bekommt bei der Wahl zum Kassenwart des Sportvereins 75 Stimmen. Dies sind 25 Prozent aller gültigen Stimmen. Wie viele Stimmen wurden insgesamt abgegeben? Berechne die Lösung mit der Formel für den Grundwert und mit dem Dreisatz.

Lösung Prozentrechnung:

Beginnen wir mit den Formeln zur Prozentrechnung. Gesucht sind alle Stimmen. Alles ist der Grundwert, daher ist G gesucht. Wir kennen aber den Anteil am gesuchten, den Prozentwert mit W = 75. Wir wissen, dass dies 25 Prozent sind. Daher haben wir p % = 25 % oder für viele sicher einfacher p = 25. Je nachdem, ob wir p oder p % nehmen können wir dies in eine der beiden oben genannten Formeln einsetzen.

Setzen wir zunächst p % ein. Wir haben damit die Formel G = W : p%. Im Zähler setzen wir W = 75 ein. Im Nenner haben wir p % = 25 %. Um dies auszurechnen muss man sich klarmachen, dass Prozent nichts anderes als Hundertstel bedeuted. Daher nehmen wir für das Ausrechnen statt dem Prozentzeichen eine Division durch 100.

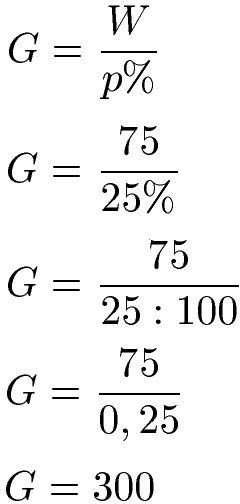
Alternativ können wir die zweite Formel nehmen und auch hier W = 75 einsetzen. Das p = 25 setzen wir ohne Prozentzeichen ein. Danach rechnen wir die Gleichung aus und erhalten ebenfalls G = 300 als Lösung.

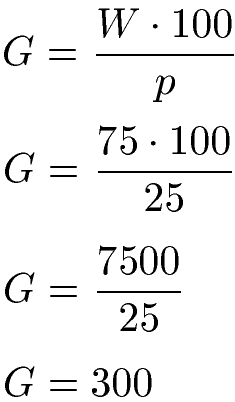
Lösung Dreisatz:

Es gibt noch eine weitere Möglichkeit das Beispiel zu berechnen. Statt der Prozentrechnung verwenden wir den Dreisatz. Bei diesem sagen wir zunächst, dass die 75 Stimmen insgesamt 25 Prozent entsprechen. Beim Dreisatz rechnet man als Erstes aus, wie viel 1 Prozent sind. Dazu teilt man beide Seiten durch 25. Wir erhalten für die 1 Prozent damit 3 Stimmen.

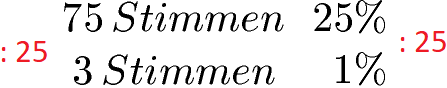
Wir interessieren uns aber nicht für 1 Prozent, sondern für 100 Prozent. Daher multiplizieren wir auf beiden Seiten mit 100. Dies entspricht zwei Nullen jeweils anzuhängen. Auch mit dieser Berechnung kommen wir auf 300 Stimmen.

Hinweis: Wer noch mehr zum Rechnen mit dem Dreisatz wissen möchte findet dies in unserem Hauptartikel unter Dreisatz.

Beispiel 2:

Marc hat in diesem Monat 12 Euro seines Taschengeldes ausgegeben. Dies sind 30 Prozent seines monatlichen Taschengeldes. Wie viel Geld bekommt er jeden Monat?

Lösung:

Gesucht ist wieder "das Ganze", also der Grundwert G. Wir wissen, dass ein Anteil von W = 12 Euro gegeben ist. Und dies sind 30 Prozent, daher ist p = 30. Wir setzen dies in die Gleichung von oben ein und rechnen die Zahlen aus. Das Ergebnis ist dann ebenfalls in Euro.

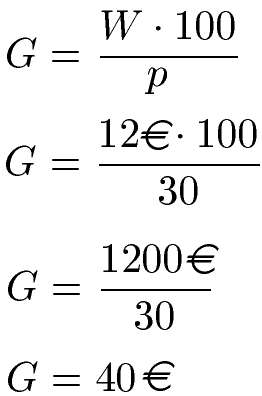
Beispiel 3:

Ein Baby-Elefant wiegt bei der Geburt 90 Kilogramm. Der Tierarzt sagt, dass dies nur 3 Prozent vom Gewicht eines ausgewachsenen Elefanten sind. Was wiegt ein ausgewachsener Elefant?

Lösung:

Wir wissen, dass der Gewichtsanteil 90 Kilogramm ist, damit ist W = 90 kg. Dies sind 3 Prozent, damit ist p = 3. Dies setzen wir in die Formel ein und berechnen das Gesamtgewicht eines erwachsenen Elefanten zu 3000 kg.

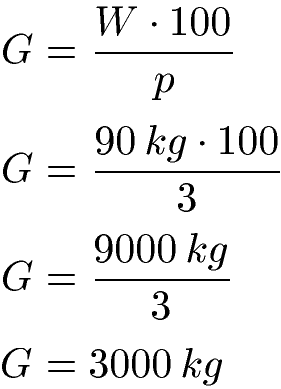
Aufgaben / Übungen Grundwert

Aufgabe 1: Frau Beck bekommt bei der Wahl zur Vorsitzenden des Tennisvereins 75 Stimmen. Dies sind 25 Prozent aller Stimmen. Wie viele Stimmen wurden insgesamt abgegeben?

• 75 Stimmen
• 400 Stimmen
• 150 Stimmen
• 300 Stimmen

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Prozentrechnung

Fragen mit Antworten Grundwert