Logarithmus Basiswechsel

Wie man einen Basiswechsel beim Logarithmus durchführt, behandeln wir hier. Dies sehen wir uns an:

• Eine Erklärung, wie man einen Basiswechsel macht.
• Beispiele zum Basiswechsel.
• Aufgaben / Übungen um das Gebiet zu üben.
• Ein Video zum Logarithmus.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns gleich den Basiswechsel an. Es hilft jedoch, wenn ihr bereits wisst, was ein Logarithmus überhaupt ist. Wer noch nie mit Logarithmus zu tun hatte wirft bitte einen Blick in die Logarithmus Grundlagen.

Basiswechsel Logarithmus Grundlagen

Manchmal kann ein Taschenrechner nur eine bestimmte Basis und man möchte einen Logarithmus dennoch berechnen. Oder man sucht einfach eine andere Basis für den Logarithmus. Die Formel mit der man den Basiswechsel durchführt ist diese:

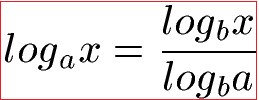
Beispiel 1:

Wir haben den Logarithmus von 16 zur Basis 4. Dieser soll auf die Basis 2 umgewandelt werden. Dazu bilden wir einen Bruch mit einem Logarithmus zur Basis 2 im Zähler und auch im Nenner. In den Zähler kommt noch die 16 und in den Nenner noch die alte Basis, also die 4.

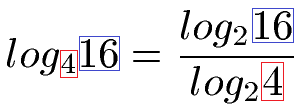
Zur Kontrolle rechnen wir beide Seiten einmal aus. Auf der linken Seite log₄¹⁶ = 2, denn 4² = 16. Auf der rechten Seite log₂16 = 4, denn 2⁴ = 16 und log₂4 = 2, denn 2² = 4.

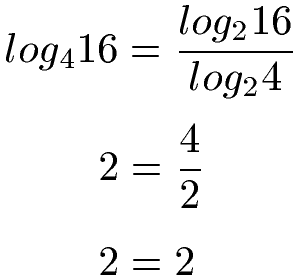
Im nächsten Abschnitt sehen wir uns ein weiteres Beispiel an.

Anzeige:

Beispiel Basiswechsel Logarithmieren

Im vorigen Beispiel konnte man beide Seiten der Gleichung einfach berechnen, indem man sich mit Potenzen und Logarithmen etwas auskennt. Aber was ist wenn das nicht klappt? Dies sehen wir uns im nächsten Beispiel einmal an.

Beispiel 2:

Wie lautet das Ergebnis dieser Aufgabe?

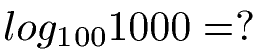
Lösung:

Ich nehme 100 hoch irgend etwas und soll 1000 bekommen. Mit 100¹ = 100 und 100² = 10000 weiß ich, das das Ergebnis irgendwo dazwischen liegen muss. Das Berechnen können wir über den Basiswechsel beim Logarithmus erreichen.

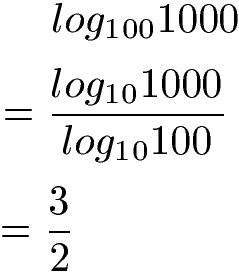
Mit der Formel von oben wandeln wir um. Wir wechseln die Basis von 100 auf 10 und berechnen die Logarithmen. Im Anschluss rechnen wir:

• Im Zähler ist log₁₀1000 = 3.
• Im Nenner log₁₀100 = 2.

Wir erhalten log₁₀1000 = 1,5.

Übungensaufgaben Basiswechsel

Aufgabe 1:

Wandle den nächsten Bruch auf die Basis 2 um. Wie lautet der neue Zähler?

• log₂32
• log₂8
• log₂4
• log₂16

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Logarithmus / Gesetze

Fragen mit Antworten Logarithmus Basiswechsel