Natürlicher Logarithmus / Logarithmus naturalis
Geschrieben von: Dennis RudolphSonntag, 14. Februar 2021 um 12:03 Uhr
Mit dem natürlichen Logarithmus befassen wir uns hier. Dies sehen wir uns an:
- Eine Erklärung, was der natürliche Logarithmus ist..
- Beispiele und Regeln zum natürlichen Logarithmus.
- Aufgaben / Übungen um das Gebiet selbst zu üben.
- Ein Video zum Logarithmus.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Der natürliche Logarithmus (lateinisch logarithmus naturalis) wird hier behandelt. Um die folgenden Inhalte zu verstehen, hilft es, die Logarithmus Grundlagen und die Eulersche Zahl zu kennen.
Natürlicher Logarithmus Erklärung
In den Grundlagen zum Logarithmus wurde unter anderem erklärt, dass es beim Logarithmus eine Basis gibt. Die Basis kann verschieden sein, zum Beispiel 2, 3 oder 10. In der nächsten Grafik mit den entsprechenden Begriffen liegt eine Basis von 2 vor.
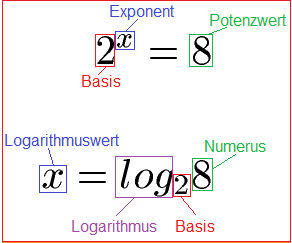
Die Basis bei einem Logarithmus kann jedoch auch eine Kommazahl bzw. eine so genannte Konstante sein. Die Eulersche Zahl ist hier eine Konstante, die regelmäßig verwendet wird. Zur Erinnerung:
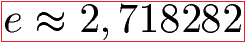
Der natürliche Logarithmus kann damit wie folgt geschrieben werden:
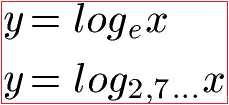
Es gibt dafür noch eine Abkürzung. Anstatt logex wird kurz ln geschrieben.
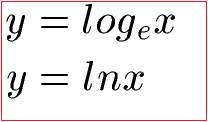
Im nächsten Abschnitt sehen wir uns noch ein Beispiel zum natürlichen Logarithmus an.
Anzeige:
Anzeigen:
Natürlicher Logarithmus Beispiel
Eine Gleichung mit natürlichem Logarithmus soll gelöst werden.
Beispiel 1:
Ermittle den Definitionsbereich und die Lösungsmenge der nächsten Gleichung.
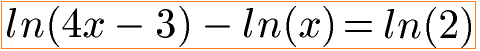
Lösung:
Wer so eine Gleichung lösen muss, sollte erst einmal einen Definitionsbereich bestimmen. Damit werden die Zahlen bestimmt, welche nicht eingesetzt werden dürfen. Wir haben dabei zwei natürliche Logarithmen mit einer Variablen. Beide müssen größer als Null sein. Bei der Berechnung sieht man, dass die strengere Bedingung x > 0,75 ist. Daher kommt dies in die Definitionsmenge.

Die Lösungsmenge soll jetzt berechnet werden. Dazu brauchen wir eine Logarithmusregel. Mit dieser Logarithmusregel können wir aus der Differenz der beiden Logarithmen einen Bruch machen. Beachtet die farbigen Rahmen in den ersten drei Zeilen. Im Anschluss müssen wir den Logarithmus loswerden. Dieser ist hier ein natürlicher Logarithmus, erkennbar an der Abkürzung ln. Die Umkehrung davon ist die E-Funktion (basierend auf der Eulerschen Zahl). Daher verwenden wir das e auf beiden Seiten der Gleichung. Im Anschluss lösen wir nach der Variablen x auf. Da x = 1,5 ist und dies größer als als die Angabe in der Definitionsmenge ist, haben wir die Lösung gefunden.
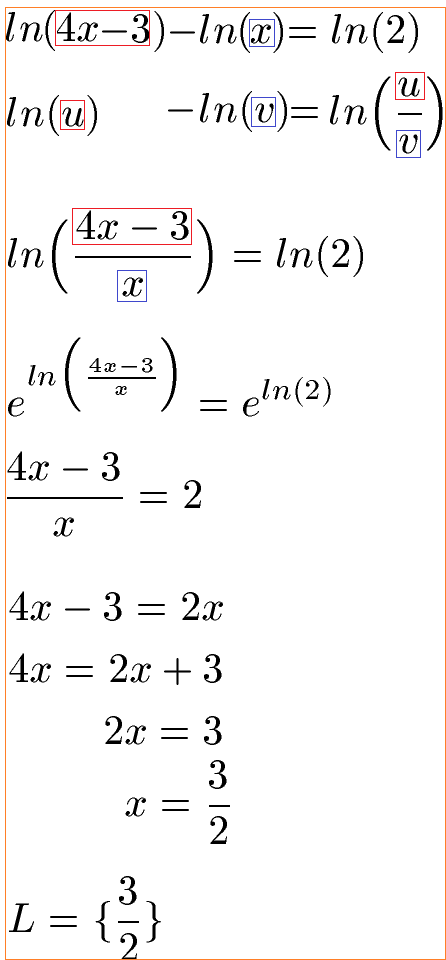
Aufgaben / Übungen natürlicher Logarithmus
Anzeigen:Video Logarithmus
Erklärungen und Beispiele
Im nächsten Video sehen wir uns dies an:
- Was ist der (natürliche) Logarithmus?
- Wozu benötigt man das Logarithmieren überhaupt?
- Spezielle Logarithmen werden erläutert.
- Einfache Aufgaben zum Logarithmus.
Nächstes Video »
Fragen mit Antworten natürlicher Logarithmus
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zum natürlichen Logarithmus an.
F: Welche Gesetze / Regeln gelten für den natürlichen Logarithmus?
A: Zur Übersicht noch einmal die Gesetze / Regeln zum natürlichen Logarithmus.
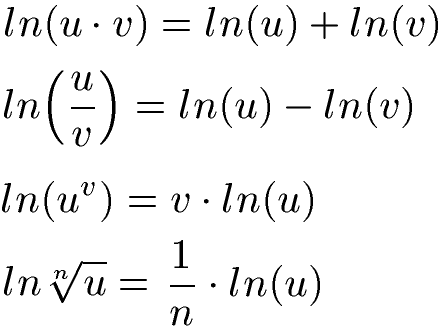
F: Wo findet der natürliche Logarithmus noch Anwendung?
A: In der Schule werden Logarithmusfunktionen und Exponentialfunktionen in der Oberstufe im Zusammenhang mit Ableitungen und Integration behandelt. Es werden dazu entsprechende Regeln erläutert und es geht darum, bei solchen Funktionen die Steigung oder die Fläche unter der Funktion zu berechnen.
F: Welche Themen rund um den natürlichen Logarithmus sollte ich mir noch ansehen?
A: Werft einen Blick auf diese Gebiete:
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
