Logarithmusfunktion

Was eine Logarithmusfunktion ist und wie diese aussieht, behandeln wir hier. Dies sehen wir uns an:

• Eine Erklärung, was eine Logarithmusfunktion ist.
• Beispiele zur Logarithmusfunktion.
• Aufgaben / Übungen zum Logarithmus.
• Ein Video zum Logarithmus.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Wer noch nie etwas vom Logarithmus gehört hat, wirft bitte erst einmal einen Blick in die Logarithmus Grundlagen. Ansonsten gleich ran an die Logarithmusfunktion.

Logarithmusfunktion Definition

Sehen wir uns erst einmal eine Definition für eine Logarithmusfunktion an:

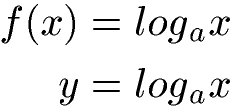
Man kann sich das Thema Logarithmusfunktion aus verschiedenen Blickwinkeln ansehen. Dies würde den Artikel extrem in die Länge ziehen. Wir sehen uns hier noch an wie man eine Logarithmusfunktion zeichnet. Wer sich für das rechnerische Lösen vom Logarithmus interessiert oder Gleichungen lösen möchte, wird jedoch gleich weiterverwiesen.

Logarithmus auflösen:

Der allgemeine Zusammenhang zwischen Potenzen und Logarithmen ist dieser:

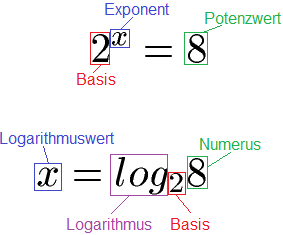
Wer so etwas lösen möchte wirft einen Blick in die Logarithmus Grundlagen.

Logarithmengesetze:

Manchmal möchte man Logarithmen umformen. Zum Beispiel aus einem Produkt eine Summe machen (und umgekehrt). Auch Brüche, Differenzen, Wurzeln und Potenzen können umgeformt werden.

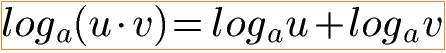
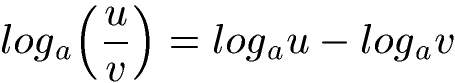
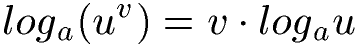
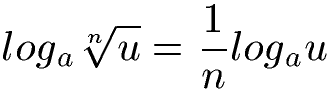
Die Logarithmengesetze und vor allem Beispiele wie man diese einsetzt findet ihr unter Logarithmengesetze.

Anzeige:

Logarithmusfunktion Beispiel

In diesem Abschnitt soll eine Logarithmusfunktion gezeichnet werden.

Beispiel 1:

Zeichne die folgende Logarithmusfunktion in ein Koordinatensystem.

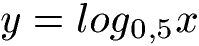
Lösung:

Beim Zeichnen von Funktionen / Gleichungen hilft es eine Wertetabelle anzulegen. Wer nicht mehr weiß wie das geht wirft noch einmal einen Blick in Wertetabelle aufstellen. Um die Funktion zu zeichnen, setzen wir von x = 0,5 bis x = 5 für x Zahlen ein und berechnen y. Es folgt erst einmal die Wertetabelle und im Anschluss wird gezeigt wie man diese berechnen kann.

Berechnung:

• y = log_0,50,5 = 1, denn 0,5¹ = 0,5
• y = log_0,51 = 0, denn 0,5⁰ = 1
• y = log_0,52 = -1, denn 0,5^-1 = 2
• y = log_0,53 = -1,58, denn 0,5^-1,58 = 3
• y = log_0,54 = -2, denn 0,5^-2 = 4
• y = log_0,55 = -2,32, denn 0,5^-2,32 = 5

Näherung ohne Logarithmus-Taste:

Wie kann man zum Beispiel die nächste Zeile berechnen ohne Logarithmus-Taste?

• y = log_0,55 = -2,32, denn 0,5^-2,32 = 5

Wir setzen für x verschiedene Zahlen ein und versuchen möglichst nahe an die 5 zu kommen:

• 0,5^-2,3 = 4,92...
• 0,5^,-2,4 = 5,278...
• 0,5^,-2,35 = 5,098...
• 0,5^,2,32 = 5

Wir zeichen den Inhalt der Wertetabelle in ein Koordinatenystem und verbinden die Punkte:

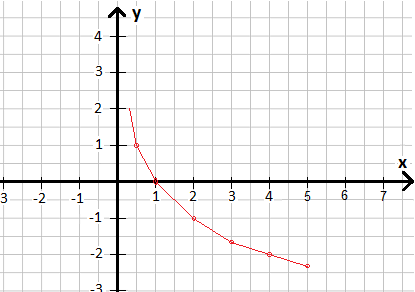
Aufgaben / Übungen Logarithmusfunktion

Aufgabe 1:

Die folgende Funktion soll gezeichnet werden. Setze x = 0,5 in die nächste Gleichung ein und berechne y.

Wie groß ist y?

• y = 2
• y = -1
• y = 0
• y = 1

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Logarithmen

Fragen mit Antworten Logarithmusfunktion