Exponentialgleichungen lösen
Geschrieben von: Dennis RudolphMontag, 15. April 2019 um 18:38 Uhr
Wie man eine Exponentialgleichung löst, lernt ihr hier. Dies sehen wir uns an:
- Eine Erklärung, was eine Exponentialgleichung ist.
- Beispiele zum Lösen von solchen Gleichungen mit Regeln.
- Aufgaben / Übungen um das Gebiet selbst zu üben.
- Ein Video zu Exponentialgleichungen.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Es gibt verschieden komplizierte Exponentialgleichungen. Um diese zu lösen sind verschiedene Vorkenntnisse nötig. Zu empfehlen ist aber auf jeden Fall, dass ihr Potenzen und Logarithmus kennt.
Exponentialgleichungen Erklärung
Klären wir zunächst die Definition einer Exponentialgleichung:
Eine Exponentialgleichung ist eine Gleichung (=) bei der in mindestens einem mathematischen Ausdruck eine Variable im Exponenten steht. Exponentialgleichungen löst man durch Exponentenvergleich, Logarithmieren und verschiedene Umformungen der Gleichung.
Im einfachsten Fall kann ein Vergleich der Exponenten die Lösung einer Exponentialgleichung liefern. Dazu müssen auf beiden Seiten Potenzen mit gleicher Basis erzeugt werden um im Anschluss auf den Exponenten zu schließen.
Beispiel 1: Exponentenvergleich
Die Gleichung 2x = 23 soll gelöst werden. Da auf beiden Seiten der Gleichung eine 2 in der Basis vorkommt, müssen wir einfach nur die Exponenten vergleichen. Da wir auf der rechten Seite der Gleichung eine 3 im Exponenten haben, brauchen wir dies auch für x auf der linken Seite.
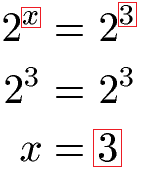
Beispiel 2: Exponentenvergleich
Im zweiten Beispiel müssen wir die rechte Seite der Exponentialgleichung umformen um eine Potenz zu erzeugen. Daher machen wir aus 81 die Potenz 34. Wir erhalten dadurch x = 4.
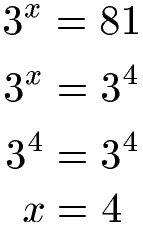
Beispiel 3: Einfacher Logarithmus
Eine weitere Möglichkeit zum Lösen von Exponentialgleichungen ist der Logarithmus. In diesem Fall ist es ein recht einfacher Logarithmus, welcher angewendet werden muss. Wir haben die Gleichung 2x = 16 und möchten nach x auflösen. Dafür brauchen wir den Logarithmus zur Basis 2, denn die Basis der Potenz 2x ist 2. Der Logarithmus von 16 zur Basis 2 ist 4, denn 24 = 16.
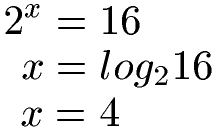
Weitere Beispiele dazu findet ihr unter Logarithmus Grundlagen.
Anzeige:
Anzeigen:
Lösen von Exponentialgleichungen
Eine etwas umfangreichere Exponentialgleichung soll hier gelöst werden.
Beispiel 4: Gleichung lösen
Wir haben die folgende Gleichung. Wie groß ist x?
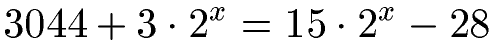
Lösung:
Zunächst kümmern wir uns um die einfachen Zahlen. Durch die Addition von 28 wird auf der linken Seite aus 3044 eine 3072. Im Anschluss holen wir 3 · 2x auf die andere Seite. Dadurch haben wir die einzelnen Zahlen vom Rest getrennt. Wir klammern 15 - 3 aus und berechnen dies zu 12. Wir teilen durch diese 12 und erhalten 256 = 2x. Mit x = 8 können wir die Exponentialgleichung lösen, denn 28 = 256.
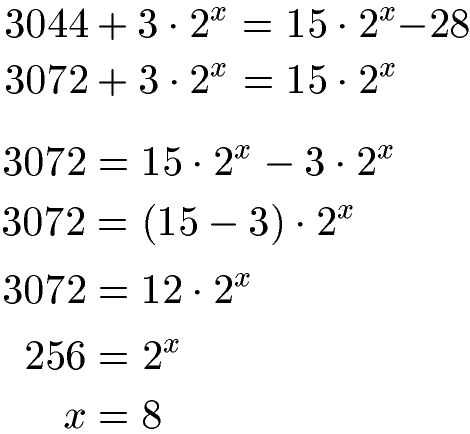
Aufgaben / Übungen Exponentialgleichungen
Anzeigen:Video Exponentialgleichungen
Erklärung und Beispiele
In diesem Video sehen wir uns das Lösen von Exponentialgleichungen an:
- Logarithmus zur Basis 2, einfaches Beispiel.
- Logarithmus zur Basis 3 mit einfachem Beispiel.
- Eine einfache Gleichung mit Ziel nach x umzuformen.
- Einfache Gleichung mit natürlichem Logarithmus.
- Etwas schwierigere Gleichung mit natürlichem Logarithmus.
Beispiele werden Stück für Stück erklärt.
Nächstes Video »
Fragen mit Antworten Exponentialgleichungen
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zu Exponentialgleichungen an.
F: Können auch Exponentialgleichungen mit e gelöst werden?
A: Weiter oben werden Exponentialgleichungen mit e im Video behandelt. Werft in dieses Video einmal einen Blick.
F: Welche Gesetze sollte ich noch kennen?
A: Zum Lösen von Exponentialgleichungen sollte jeder den Logarithmus kennen. Teil vom Logarithmieren sind die Logarithmengesetze. Diese hier solltet ihr kennen:
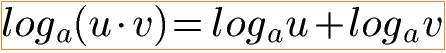
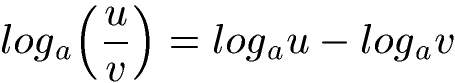
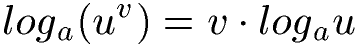
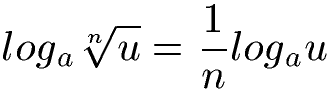
Noch keine Ahnung davon? Ihr möchtet mehr zum Logarithmieren lernen? Werft einen Blick auf diese Inhalte:
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
