Exponentialfunktionen: Eigenschaften, zeichnen...

Was eine Exponentialfunktion ist, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, welche Eigenschaften eine Exponentialfunktion hat.
• Beispiele und Anwendungen für Exponentialfunktionen.
• Aufgaben / Übungen um das Gebiet selbst zu üben.
• Ein Video zu solchen Funktionen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Um die Exponentialfunktionen zu verstehen, solltet ihr bereits wissen, was eine Potenzfunktion ist. Wer davon noch keine Ahnung hat, wirft bitte einen Blick in die Grundlagen Potenzen.

Exponentialfunktionen Eigenschaften

Es gibt verschiedene Arten von Exponentialfunktionen und auch die Definitionen (Eigenschaften) von Exponentialfunktionen können daher etwas verschiedene aussehen. Gemeinsam haben die Exponentialfunktionen, dass die Variable im Exponenten vorkommt. Im einfachsten Fall ist die Funktion bzw. Gleichung wie folgt:

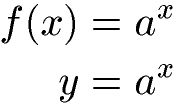
In vielen Fällen darf auch noch eine Konstante davor stehen, mit welcher die Potenz multipliziert wird. Damit verändert sich die Funktion / Gleichung zu:

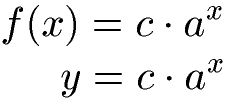
Das "c" ist dabei eine feste Konstante. Mit "a" haben wir die Basis der Potenz und x ist eben die Variable im Exponenten.

Natürliche Exponentialfunktion:

Eine besondere Form der Exponentialfunktion ist die natürliche Exponentialfunktion. Man bezeichnet diese als natürlich, da als Basis die Eulersche Zahl "e" verwendet wird. Die ganz einfache E-Funktion ist einfach y = e^x. Jedoch kann die Funktion erweitert werden (mit c und b wie in der zweiten Gleichung zu sehen ist).

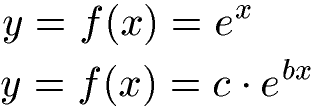
Anzeige:

Exponentialfunktion Beispiel

Menschen denken in der Regel linear und nicht exponentiell. Dies sorgt dafür, dass Menschen sich exponentielles Wachstum nicht intuitiv vorstellen können. Daher rechnen wir.

Beispiel 1:

Wir haben die folgende Gleichung. Lege eine Wertetabelle für x = 1 bis x = 10 an und berechne y. Zeichne im Anschluss die Funktion:

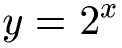
Lösung:

Wir legen eine Wertetabelle von x = 1 bis x = 10 ein. In die Gleichung setzen wir für x verschiedene Zahlen ein und berechnen y:

• 2¹ = 2
• 2² = 2 · 2 = 4
• 2³ = 2 · 2 · 2 = 8
• 2⁴ = 2 · 2 · 2 · 2 = 16
• ...

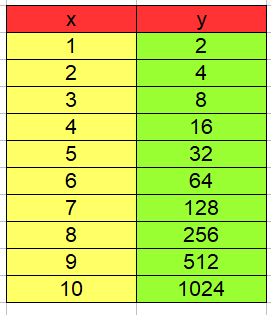
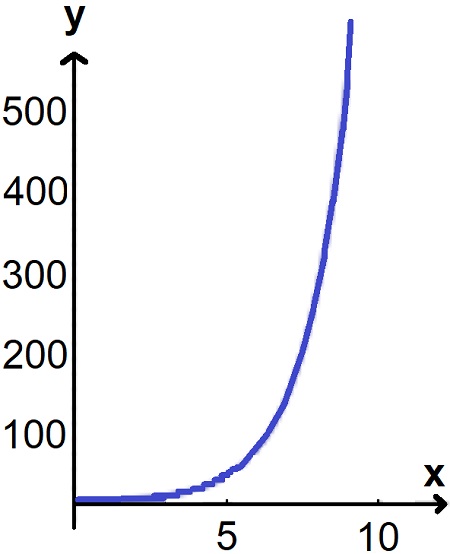
Zeichnet man die Funktion in ein Koordinatensystem ein, erhält man diesen Verlauf:

Aufgaben / Übungen Exponentialfunktion

Aufgabe 1:

Welche der folgenden Gleichungen ist eine Exponentialfunktion?

• y = 4^x
• y = 4x
• y = x⁴
• y = 4 - y

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video E-Funktion / Exponentialfunktion

Fragen mit Antworten Exponentialfunktion