Kongruenzsatz SSS, SWS, WSW und SSW
Geschrieben von: Dennis RudolphSamstag, 02. Juni 2018 um 18:23 Uhr
Was man unter der Kongruenz bzw. den Kongruenzsätzen versteht, wird hier einfach erklärt. Das Zeichnen von Dreiecken mit einem Kongruenzsatz findet ihr hingegen unter Dreieck zeichnen. Dies sehen wir uns an:
- Eine Erklärung was Kongruenz und die Sätze dazu sind.
- Beispiele für die Kongruenzsätze SSS, SWS, WSW und SSW.
- Aufgaben / Übungen damit ihr dies selbst üben könnt.
- Ein Video zu diesem Thema
- Ein Frage- und Antwortbereich zu diesem Gebiet.
Tipp: Wer lernen möchte mit den Kongruenzsätzen Dreiecke zu zeichnen, der findet Erklärungen und Beispiele dazu unter Dreieck konstruieren (zeichnen).
Erklärung Kongruenzsätze
Was ist überhaupt Kongruenz und was macht man damit?
Zwei Dreiecke sind kongruent zueinander, wenn diese Deckungsgleich sind. Von einem Dreieck zum anderen Dreieck kommt man durch drehen, verschieben oder spiegeln. Die Regeln für Kongruenz fasst man mit vier Kongruenzsätzen zusammen.
Beispiel Kongruenz:
Die beiden folgenden Dreiecke sind kongruent zueinander, denn man kommt von einem Dreieck zum anderen durch Verschieben und Drehen.
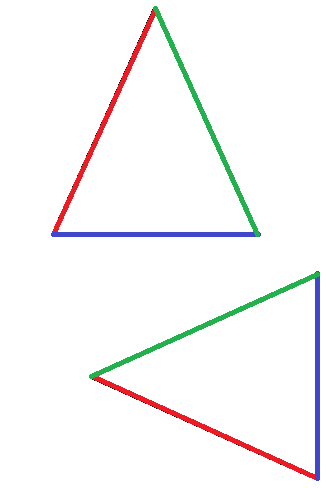
Sehen wir uns die vier Kongruenzsätze mit Beispiel einmal an.
Kongruenzsatz SSS mit Beispiel:
Beginnen wir mit dem Kongruenzsatz SSS. Dieser besagt, dass wenn alle drei Seiten der Dreiecke übereinstimmen, dass diese kongruent sind. Beispiel: Wir haben ein Dreieck, von dem die Länge aller drei Seiten bekannt sind. Dieses drehen und verschieben wir einfach und erhalten zwei Dreiecke, die zueinander kongruent sind.
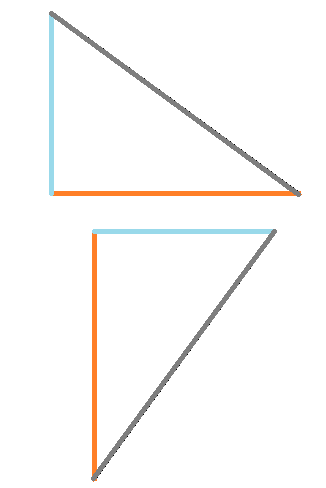
Wie man mit den Kongruenzsätzen Dreiecke zeichnet, lernt ihr unter Dreieck konstruieren (zeichnen).
Anzeige:
Anzeigen:
Beispiele Kongruenzsätze
In diesem Abschnitt sehen wir uns drei weitere Kongruenzsätze mit Beispiel an.
Kongruenzsatz SWS mit Beispiel:
Sehen wir uns als nächstes den Kongruenzsatz SWS an. Bei diesem geht es darum, dass zwei Seiten und der dabei eingeschlossene Winkel übereinstimmen. Die nächste Grafik zeigt so zwei unvollständige Dreiecke.
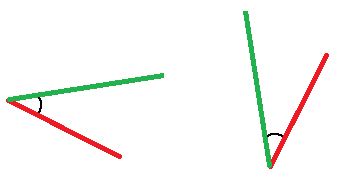
Ist dies der Fall und man zeichnet die Dreiecke fertig, sind diese ebenfalls kongruent zueinander. Grund dafür ist, dass die drei Seiten gleichlang sind bei beiden Dreiecken und alle Winkel ebenfalls entsprechend gleich groß.
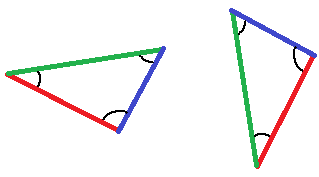
Kongruenzsatz WSW mit Beispiel:
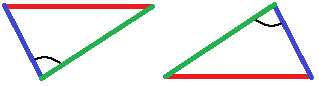
Der dritte Fall ist der Kongruenzsatz WSW. Dabei müssen zwei Winkel und die eingeschlossene Seite übereinstimmen. Die nächste Grafik zeigt wieder zwei unvollständige Dreiecke. Hier ist eine Seite gegeben und zwei Winkel sind angedeutet.

Zeichnet man die Dreiecke fertig, erhält man ebenfalls zwei zueinander kongruente Dreiecke. Diese sind gegenüber der vorigen Grafik verschoben, damit das Bild nicht zu groß wird.
Kongruenzsatz SSW mit Beispiel:
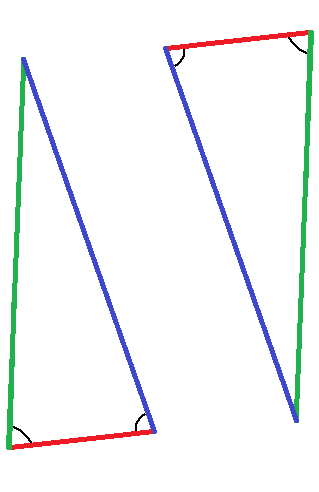
Der letzte Kongruenzsatz ist SSW. Hier sind zwei Dreiecke kongruent zueinander, wenn zwei Seiten und der der längeren Seite gegenüberliegende Winkel übereinstimmen. Die nächste Grafik zeigt eine lange Seite in rot und eine kürzere Seite in blau. Außerdem ist ein Winkel bekannt, welcher der längsten Seite (rot) gegenüberliegt.

Zeichnet man die Dreiecke fertig, erhält man ebenfalls zwei zueinander kongruente Dreiecke.
Aufgaben / Übungen Kongruenzsätze
Anzeigen:Videos Kongruenzsätze
Video SWW
In diesem Video wird anhand eines Beispiels erklärt, wie ein Dreieck nach SWW konstruiert wird:
- In dem Video wird die Herangehensweise gezeigt, mit den vorhandenen Angaben ein Dreieck zu konstruieren.
- Es beginnt mit der Konstruktion der gegebenen Seite als horizontale Linie. An diese wird der gegebene Winkel angetragen.
- Durch Parallelverschiebung und Winkelkonstruktion entsteht das fertige Dreieck.
Als Hilfsmittel für dieses Video empfehlen wir euch ein Geodreieck, ein Zirkel, einen spitzen Bleistift und kariertes Papier. Video-Quelle: Youtube.com
Nächstes Video »
Fragen mit Antworten Kongruenzsätze
In diesem Abschnitt sehen wir uns Fragen mit Antworten zu den Kongruenzsätzen an.
F: Gibt es den Kongruenzsatz WWW?
A: Nein. Bei drei Winkeln gibt es keine Kongruenz. Grund dafür ist, dass die Dreiecke trotz drei gleich großer Winkel eine unterschiedliche Größe haben können.
F: Kann ich mit den Kongruenzsätzen auch Dreiecke zeichnen?
A: Wie man dies macht lernt ihr unter Dreieck konstruieren (zeichnen).
F: Welche Themen sollte ich mir als nächstes ansehen?
A: Die Kongruenzsätze sind Teil der Geometrie. In diesem Bereich haben wir noch weitere Inhalte verfügbar, wie zum Beispiel diese hier:
- Winkel Mathematik
- Winkelarten / Winkeltypen
- Winkel messen
- Winkel zeichnen
- x-y-Koordinatensystem
- Begriffe Geometrie
- Figur drehen, verschieben und spiegeln
- Kreiszahl Pi
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
