Prisma Formeln: Volumen, Oberfläche ...

Wie man die Formeln zum Prisma verwendet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung was ein Prisma ist und wie man an diesem rechnet.
• Beispiele zu Berechnen von Volumen, Oberfläche und Mantelfläche.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zum Prisma.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen wir uns gleich die Berechnung von Prismen in der Mathematik an. Es ist hilfreich, wenn ihr bereits wisst, was eine Fläche und was ein Volumen ist. Noch keine Ahnung? Seht einmal in Fläche Rechteck und Volumeneinheiten umrechnen.

Erklärung Prisma Formeln

Klären wir einmal kurz, was ein Prisma überhaupt ist. Definition Prisma:

Beispiel Prisma:

Wir zeichnen eine Grundfläche, zum Beispiel ein Dreieck:

Wir zeichnen in etwas Entfernung die Grundfläche noch einmal (jetzt Deckfläche genannt):

Wir verbinden die Eckpunkte:

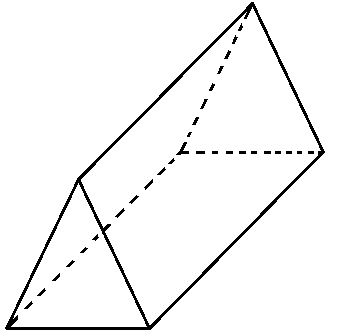
Prisma Formeln für Volumen, Oberfläche und Mantelfläche:

Das Volumen gibt an, wie viel in das Prisma reinpasst. Dabei ist V das Volumen, G die Grundfläche und h die Höhe.

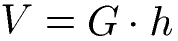
Die Oberfläche gibt die Summe aller Flächen vom Prisma an. Dabei ist O die Oberfläche, G die Grundfläche und M die Mantelfläche.

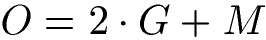
Die Mantelflächen sind alle Flächen, die nicht zum Boden (Grundfläche) oder Deckel (Deckfläche) gehören. In der nächsten Formel ist M die Mantelfläche, O die Oberfläche und G die Grundfläche.

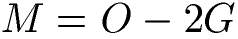
Es gibt zahlreiche verschiedene Arten von Prismen. Quader, Würfel oder auch eine Dreiecks- bzw. Trapezsäule sind Prismen. Dies macht auch den Einsatz der Formeln / Gleichungen für Volumen, Oberfläche und Mantelfläche schwieriger. Daher sehen wir uns besser einige Beispiele an.

Anzeige:

Beispiele Formeln: Volumen, Oberfläche, ...

Sehen wir uns einige Beispiele zu Volumen, Oberfläche und Mantelfläche an.

Beispiel 1: Dreiseitiges Prisma

Gegeben sei das folgende dreiseitige Prisma. Wie groß ist sein Volumen?

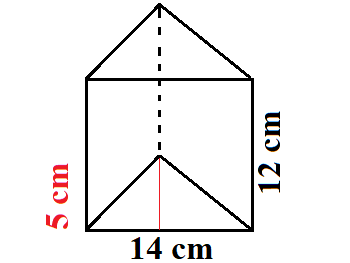
Lösung:

Wir haben ein Dreieck als Grundfläche. Dieses ist 14 cm breit und 5 cm "hoch". Die Höhe ist hier in rot eingezeichnet. Wir berechnen die Fläche von einem Dreieck mit der Breite davon multipliziert mit der Höhe darauf. Und durch zwei müssen wir noch teilen. Wer die allgemeine Formel nicht kennt sieht bitte in Fläche Dreieck. Wir berechnen damit die Grundfläche unten wie folgt:

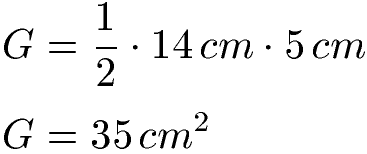
Um das Volumen zu berechnen, müssen wir die Grundfläche noch mit der Höhe multiplizieren:

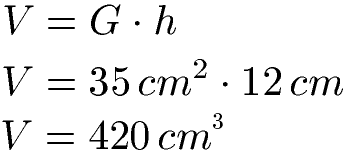
Dieses Prisma hat ein Volumen von 420 Kubikzentimeter.

Beispiel: Quader als Prisma

Wir haben ein Prisma, welches auch ein Quader ist. Es ist 14 Zentimeter hoch, 12 cm breit und 16 cm tief. Wie groß sind Oberfläche, Volumen und Mantelfläche von diesem Prisma?

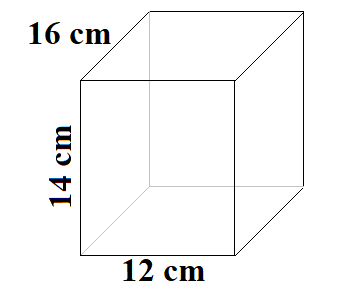
Lösung:

Die Grundfläche ist ein Rechteck. Wir beginnen damit dieses zu berechnen. Die Fläche von einem Rechteck erhält man mit Länge multipliziert mit der Breite.

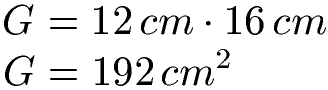
Um das Volumen zu erhalten, müssen wir die Grundfläche noch mit der Höhe (14 cm) multiplizieren.

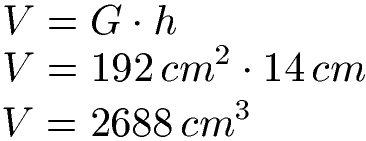
Also nächstes berechnen wir die Mantelfläche. Das ist die Fläche ohne Boden und Deckel. Dies sind die Flächen vorne und hinten sowie links und rechts, Das sind jeweils Rechtecke. Dabei sind die Flächen links und rechts gleich groß und vorne und hinten gleich groß. Alles sind Rechtecke, daher sind die Flächen auch wieder Länge mal Breite.

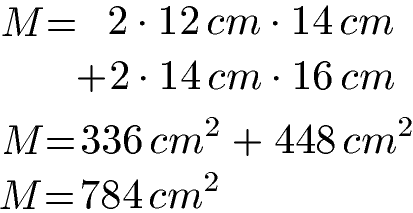
Damit rechnen wir jetzt die Oberfläche vom Prima aus:

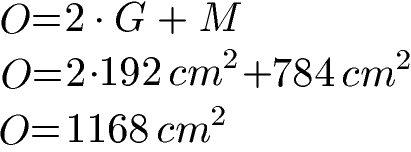
Die Oberfläche beträgt damit 1168 cm².

Aufgaben / Übungen zum Prisma

Aufgabe 1: Die Grundfläche des Prisma besteht aus einem rechtwinkligen Dreieck. Die Katheten sind 9 cm und 12 cm lang und die Höhe beträgt 20 cm. Wie groß ist das Volumen?

• 976 cm³
• 1140 cm³
• 1080 cm³
• 1020 cm³

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Prisma

Fragen mit Antworten Prisma Formeln