Schnittpunkt x-Achse

Wie kann man den Schnittpunkt mit der x-Achse berechnen? Genau dies sehen wir uns in den nächsten Abschnitten an. Folgende Inhalte werden angeboten:

• Eine Erklärung, was man unter einem Schnittpunkt mit der x-Achse versteht.
• Beispiele zum Berechnen von Schnittpunkten.
• Übungen damit ihr dies alles selbst üben könnt.
• Ein Video zum Berechnen von Schnittpunkten.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns hier an, wie man für lineare Funktionen (Gleichungen) bzw. quadratische Funktionen (Gleichungen) den Schnittpunkt mit der-Achse findet. Wer von diesen beiden Gleichungsarten noch nie gehört hat, der sieht bitte erst einmal in lineare Gleichungen lösen und quadratische Funktion lösen rein.

Schnittpunkt mit x-Achse: lineare Funktion

Beginnen wir mit dem Schnittpunkt mit der x-Achse bei einer linearen Funktion. Eine lineare Funktion bzw. eine lineare Gleichung hat die Form y = mx + b oder f(x) = mx + b. In der nächsten Grafik ist ein Beispiel zu sehen, bei dem dieser Punkt in rot eingekreist wurde.

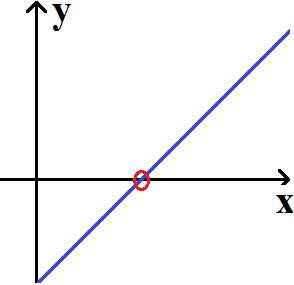
Welche Eigenschaft hat dieser Punkt?

Lineare Gleichung / Funktion Beispiel 1:

Wo liegt der Schnittpunkt mit der x-Achse bei der Gleichung y = x - 2?

Lösung: Wir wissen, dass wir zum Auffinden der Nullstelle y = 0 setzen müssen.

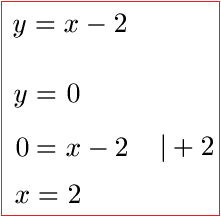
Wir haben bei x = 2 den Schnittpunkt mit der x-Achse. Und diese Stelle zeichnet sich dadurch aus, dass hier y = 0 ist. Also ist der Punkt der Nullstelle P (2;0).

Lineare Gleichung / Funktion Beispiel 2:

Wo liegt der Schnittpunkt der Funktion y = 4x - 4?

Lösung: Auch hier setzen wir y = 0 und berechnen dann x.

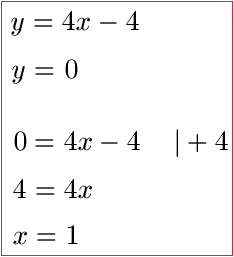
Bei x = 1 liegt die Nullstelle. Wir wissen, dass hier auch y = 0 ist. Daher ist der Punkt der Nullstelle P (1;0).

Anzeige:

Schnittpunkt mit x-Achse quadratische Funktion

Auch eine quadratische Gleichung / Funktion kann einen oder mehrere Schnittpunkte mit der x-Achse aufweisen. Die nächste Grafik zeigt den Graphen einer quadratischen Funktion. Es gibt zwei Nullstellen, welche beide mit einem roten Kreis markiert wurden.

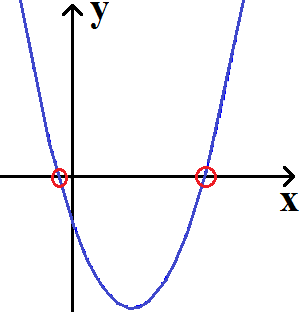
Was sollte man dazu wissen?

Es gibt mehrere Möglichkeiten eine quadratische Gleichung zu lösen um die Schnittpunkte mit der x-Achse zu finden. Eine Variante soll hier mit der PQ-Formel gezeigt werden.

Die PQ-Formel

Bevor wir die PQ-Formel verwenden können, sollte ihr natürlich erst einmal wissen, wie die PQ-Formel überhaupt aussieht. Um diese einsetzen zu können, muss man zunächst dafür sorgen, dass wir bei der quadratischen Funktion vor x² eine 1 stehen haben und die Gleichung auf die Form mit = 0 gebracht wird. Danach kann man p und q ablesen und einfach einsetzen. Zunächst die Lösungsgleichung, danach ein Beispiel.

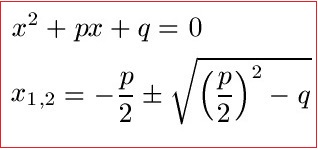
Beispiel 3: Schnittpunkt x-Achse quadratische Funktion

Wir wollten das Beispiel 3x² + 9x + 5 = - 1 lösen um die Schnittpunkte mit der x-Achse (also die Nullstellen) zu finden:

• Wir wissen, dass wir die Gleichung in der Form = 0 brauchen, daher rechnen wir zunächst +1 um die -1 auf der rechten Seite zu beseitigen und = 0 zu erhalten.
• Auch brauchen wir vor dem x² eine 1, also 1x² und nicht wie hier 3x². Daher teilen wir die Gleichung durch 3.
• Im nächsten Schritt können wir p und q einfach ablesen und in die Formel für die Lösung aus der letzten Grafik einsetzen.
• Wir berechnen den Bruch vor der Wurzel und alles unter der Wurzel.
• Vor dem Wurzelzeichen steht ein plus (+) und ein minus(-). Wir berechnen x₁ mit dem plus und x₂ mit dem minus.
• Wir erhalten mit der Berechnung zwei Lösungen. Dies sind die beiden Nullstellen, sprich die Schnittpunkte mit der x-Achse.

Ihr braucht zusätzliche Beispiele und Erklärungen zur PQ-Formel? Werft einen Blick auf den Artikel PQ-Formel.

Aufgaben / Übungen Schnittpunkt x-Achse

Aufgabe 1: Zunächst ein kurzer Hinweis: Wer eine Aufgabe oder Frage nicht mag, kann auf "Überspringen" klicken. Bevor wir Rechnen erst einmal ein paar Fragen zum Einstieg: Welche Eigenschaft haben Nullstellen gemeinsam (in einem normalen x-y-Koordinatensystem wie im Artikel verwendet)?

• a = 0
• x = 0
• y = 0
• z = 0

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Schnittpunkt x-Achse

Fragen mit Antworten Schnittpunkt x-Achse