Schnittpunkt y-Achse

Wie kann man den Schnittpunkt mit der y-Achse berechnen? Genau dies sehen wir uns in den nächsten Abschnitten an. Folgende Inhalte werden angeboten:

• Eine Erklärung, was man unter einem Schnittpunkt mit der y-Achse versteht.
• Beispiele zum Berechnen von Schnittpunkten mit der y-Achse.
• Übungen damit ihr dies alles selbst üben könnt.
• Ein Video zum Berechnen von Schnittpunkten.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns hier an, wie man für lineare Funktionen (Gleichungen) bzw. quadratische Funktionen (Gleichungen) den Schnittpunkt mit der y-Achse findet. Wer von diesen beiden Gleichungsarten noch nie gehört hat, wirft bitte erst einmal einen Blick in die Artikel lineare Gleichungen lösen und quadratische Funktion lösen.

Erklärung: Schnittpunkt y-Achse lineare Funktion

Was ist ein Schnittpunkt mit der y-Achse und wie berechnet man diesen? Die nächsten beiden Grafiken zeigen wo sich die Schnittpunkte mit der y-Achse befinden. Die obere Grafik ist eine lineare Funktion (Gleichung). Der Verlauf des Funktionsgraphen schneidet die y-Achse. Die entsprechende Stelle wurde mit einem roten Kreis markiert.

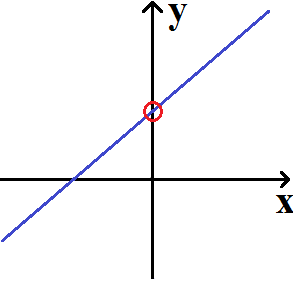
Auch bei einer quadratischen Funktion (Gleichung) kann man sich auf die Suche nach einem Schnittpunkt mit der y-Achse machen. In der nächsten Grafik ist auch hier dieser Punkt mit einem roten Kreis markiert.

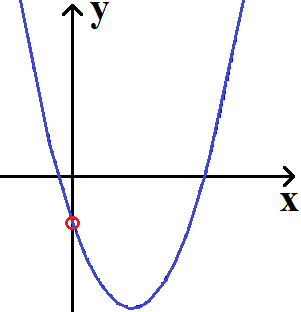
Wie findet man die Schnittpunkte mit der y-Achse? Dazu gibt es grundsätzlich zwei Möglichkeiten:

1. Man zeichnet den Funktionsgraphen (in ein Koordinatensystem) und findet dann mit Blick auf den Graphen die Nullstelle. Nachteil: Manchmal lässt sich dieser Punkt nicht so genau ablesen.
2. Wir nehmen die Funktion bzw. Gleichung und setzen x = 0 ein. Denn wie man an den Funktionsgraphen sehen kann, ist der Schnittpunkt immer da wo x = 0 ist. Damit können wir y ausrechnen.

Anzeige:

Erklärung: Schnittpunkt y-Achse lineare Funktion

In diesem Abschnitt sehen wir uns an, wie man bei einer linearen Funktion oder einer quadratischen Funktion die Schnittpunkte mit der y-Achse berechnet.

Beispiel 1: Lineare Funktion

Gegeben sei die Funktion y = 3x + 2. Wo liegt der Schnittpunkt mit der y-Achse?

Lösung:

Wir nehmen die lineare Gleichung und setzen x = 0 ein. Wir errechnen damit y = 2.

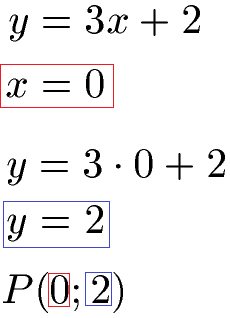
Der Schnittpunkt mit der y-Achse liegt bei x = 0 und y = 2.

Beispiel 2: Quadratische Funktion

Wir haben die quadratische Funktion y = 2x² -3x + 6. Wo liegt der Schnittpunkt mit der y-Achse?

Lösung:

Wir setzen bei dieser quadratischen Gleichung x = 0 und berechnen damit y = 6. Der Schnittpunkt liegt bei P(0;6).

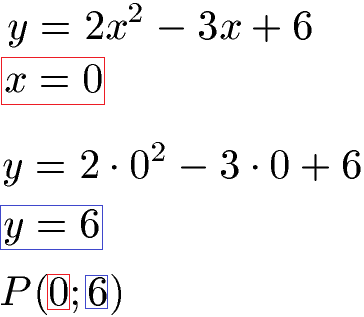
Video Schnittpunkt

Anzeigen:

Fragen mit Antworten Schnittpunkt y-Achse