Gleichungen / Gleichungssysteme zeichnerisch lösen

Wie kann man Gleichungen zeichnerisch (grafisch) lösen? Genau dies sehen wir uns in den nächsten Abschnitten an. Folgende Inhalte werden angeboten:

• Eine Erklärung, was das zeichnerische Lösen von Gleichungen bedeutet.
• Beispiele zum grafischen Lösen von Gleichungssystemen.
• Übungen damit ihr dies alles selbst üben könnt.
• Ein Video zum Lösen von Gleichungen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns hier an wie man Gleichungen zeichnerisch / grafisch lösen kann. Wer die folgenden Inhalte nicht versteht, der sieht bitte erst einmal in die Artikel Wertetabelle aufstellen und Gleichungssysteme rein.

Erklärung: Gleichungen zeichnerisch lösen

In der Mathematik hat man manchmal nicht nur eine Gleichung sondern, sondern zwei Gleichungen und mehr. Dies bezeichnet man auch als Gleichungssystem. Man kann solche Gleichungssysteme sowohl rechnerisch als auch zeichnerisch lösen.

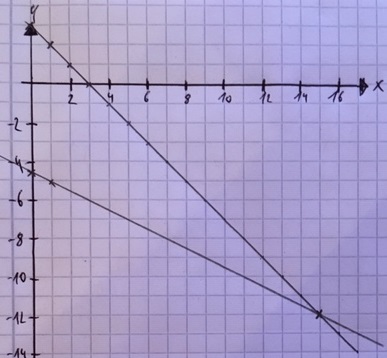
Die nächste Grafik zeigt den Schnittpunkt zweier Gleichungen. Diese beiden Gleichungen haben damit eine Lösung.

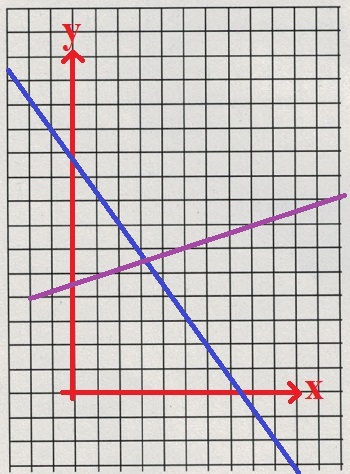
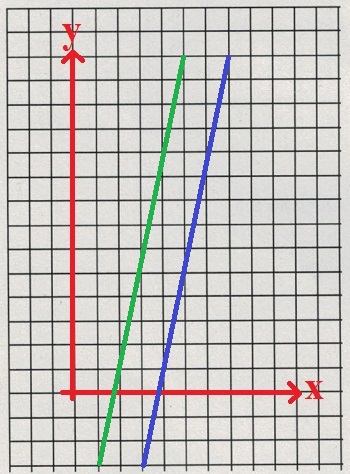
Der nächste Fall zeigt zwei Gleichungen / Gleichungssysteme ohne Lösung (da kein Schnittpunkt).

Anzeige:

Beispiel: Gleichungssystem grafisch lösen

In diesem Abschnitt sehen wir uns ein Beispiel an, wie man zwei Gleichungen (Gleichungssystem) grafisch lösen kann.

Beispiel 1: Gleichungssystem grafisch lösen

Wir haben die beiden folgenden Gleichungen mit jeweils x und y. Löse diese zeichnerisch.

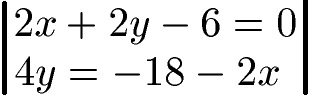
Lösung:

Zunächst bringen wir beide Gleichungen auf die "gewohnte" Form, sprich wir lösen beide Gleichungen nach y auf.

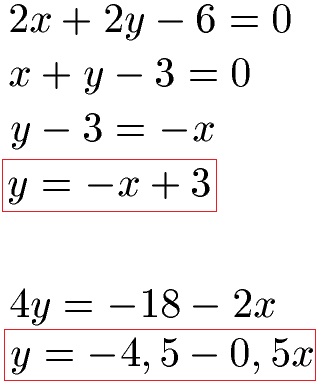
Wir setzen in beide Gleichungen jeweils x = 0 und x = 1 ein und berechnen y. Dies ist ausreichend, da es sich jeweils um eine lineare Funktion handelt.

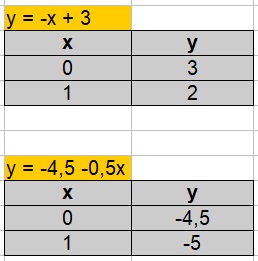
Kennen wir zwei Punkte der linearen Gleichung bzw. linearen Funktion können wir einfach die Punkte einzeichnen und verbinden und in beide Richtungen verlängern.

Der gemeinsame Schnittpunkt liegt damit bei x = 15 und y = -12.

Aufgaben / Übungen Gleichungen grafisch lösen

Aufgabe 1: Ein Gleichungssystem wurde gezeichnet und es gibt keinen Schnittpunkt. Was bedeutet dies für die Gleichungen?

• Zwei gemeinsame Lösungen
• Keine gemeinsame Lösung
• Eine gemeinsame Lösung
• Drei gemeinsame Lösungen

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Gleichung zeichnen

Fragen mit Antworten Gleichungssystem grafisch lösen