Binärzahlen mit Umrechnung

Was Binärzahlen sind und wie man solche Zahlen umwandelt, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung was Binärzahlen sind und wozu sie benutzt werden.
• Beispiele um Dezimalzahlen in Binärzahlen umzuwandeln und umgekehrt.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zu Binärzahlen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Als Vorwissen reicht es eigentlich, wenn ihr ganz einfache Zahlen von 1 bis 100 kennt. Wer davon noch keine Ahnung hat sieht bitte in die natürlichen Zahlen rein.

Erklärung Binärzahlen

Aus dem Alltag und der Schule kennt man das Dezimalsystem. Dieses besteht aus 10 verschiedenen Zahlen: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Zählt man nach der 9 weiter werden die Zahlen zusammengesetzt. Die 10 besteht aus 1 und 0. Die 11 besteht aus 1 und 1. Diese bedeutet, dass ab der 10 die Zahlen zusammengesetzt werden. Wird die 9 am Ende einer Zahl erreicht und es soll weiter gezählt werden, dann steht eine 0 auf der letzten Stelle und die Stelle davor wird ebenfalls hochgezählt.

Binärzahlen:

Ein Computer, Handy / Smartphone etc. rechnet anders. Diese arbeiten mit einem Binärsystem. Bei den Binärzahlen gibt es nur 0 und 1. Daher müssen alle Zahlen aus 0 und 1 zusammengesetzt werden. Um klar zu machen, ob es sich um eine Dezimalzahl oder eine Binärzahl handelt, fügt man eine kleine zusätzliche Zahl hinzu. Bei einer Dezimalzahl wird eine kleine 10 hinzugefügt, bei der Binärzahlen ist es eine 2.

Alternativ kann man in einer Tabelle auch drüber schreiben, ob es sich um eine Dezimalzahl oder Binärzahl handelt. Um zu verstehen wie Binärzahlen aufgebaut sind, sehen wir uns erst einmal eine kleine Tabelle mit den Binärzahlen bis 15 an.

Auf der linken Seite in gelb markiert findet ihr die Dezimalzahl. Rechts davon die Binärzahlen. Um die Dezimalzahlen bis 15 darzustellen, werden vier Stellen in Binär benötigt.

• Auf der Stelle ganz rechts kann maximal 1 dargestellt werden.
• Auf der zweithöchsten Stelle maximal 2.
• Auf der dritthöchsten Stelle maximal 4.
• Auf der dritthöchsten Stelle maximal 8.
• Diese 1, 2, 4, 8 wurden grün markiert.
• Weitere Stellen falls benötigt wären 16, 32, 64, 128 etc. Es wird immer verdoppelt.

Mit diesen Stellen werden die Zahlen nun "zusammengebaut". Werft kurz einen Blick auf die Tabelle, im Anschluss werden die Zahlen einzeln vorgestellt:

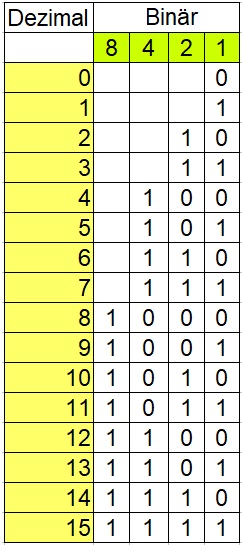
So werden die Binärzahlen mit den Stellen zusammengesetzt:

• 0: 0 ist 0.
• 1: 1 ist 1.
• 2: Hier brauchen wir nur die 2. Daher auf die 2er-Stelle eine 1.
• 3: Hier brauchen wir die 2 und die 1. Daher auf die 2er-Stelle und 1er-Stelle eine 1.
• 4: Hier brauchen wir nur die 4. Daher auf die 4er-Stelle eine 1.
• 5: Hier brauchen wir die 4 und die 1. Daher auf 4er-Stelle und 1er-Stelle eine 1.
• 6: Hier brauchen wir die 4 und die 2. Daher auf die 4er-Stelle und die 2er-Stelle eine 1.
• 7: Hier brauchen wir die 4, die 2 und die 1. Daher auf diesen drei Stellen eine 1.
• 8: Hier brauchen wir nur die 8, daher auf die 8er-Stelle eine 1 und der Rest 0.
• 9: Hier brauchen wir die 8 und die 1, daher auf der 8er-Stelle und der 1er- Stelle eine 1.
• Und so weiter....

Anzeige:

Beispiele Umwandlung Binärzahlen

In diesem Abschnitt sehen wir uns an wie man Binärzahlen in Dezimalzahlen verwandelt und umgekehrt.

Beispiel 1: Binärzahl in Dezimalzahl

Die Binärzahlen 101 sowie 1010 sollen in Dezimalzahlen umgewandelt werden.

Lösung für 101:

Wir arbeiten mit der Potenzschreibweise. Dazu müssen wir jede Stelle einzeln in eine Potenz umschreiben und am Ende addieren. Ich markiere die Berechnung farbig um sie besser nachvollziehbar zu machen.

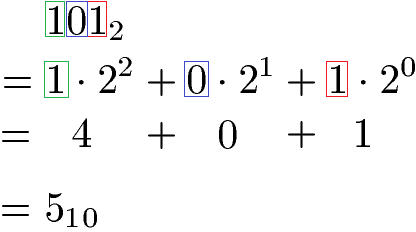
Binär 101 entspricht damit dezimal 5.

Lösung für 1010:

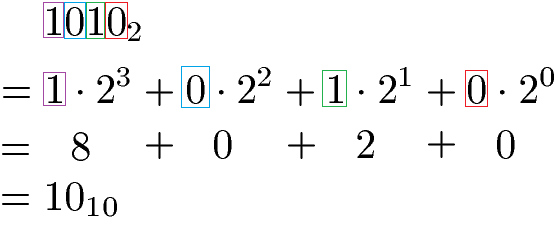
Binär 1010 entspricht dezimal 10.

Beispiel 2: Dezimalzahl in Binärzahl

Die Dezimalzahlen 12 und 45 sollen in Binärzahlen umgewandelt werden.

Lösung 12:

Wir nehmen die jeweilige Dezimalzahl und teilen durch 2. Dabei entsteht ein Quotient mit Rest oder ohne Rest. Der Quotient wird dann wieder durch 2 geteilt bis er 0 ist. Der entstehende Rest ist unsere Binärzahl.

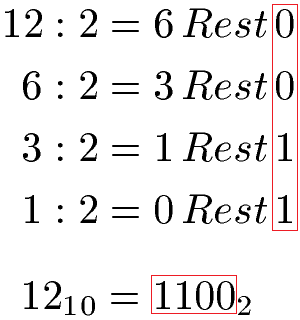
Aus der Dezimalzahl 12 wird die Binärzahl 1100.

Lösung 45:

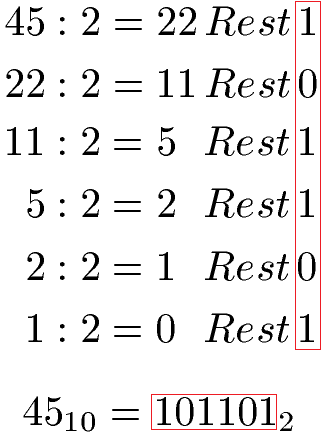
Die Zahl 45 dezimal ist 101101 binär.

Aufgaben / Übungen Binärzahlen

Aufgabe 1: Bei den Binärzahlen gibt es nur die Zahlen 0 und ____ ?

• 4
• 2
• 1
• 3

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 5 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Binärzahlen

Fragen mit Antworten zu Binärzahlen