Parabel verschieben, stauchen und strecken

Wie man eine Parabel verschieben, stauchen oder strecken kann, lernt ihr hier. Zum Inhalt:

• Eine Erklärung, wie man eine Parabel hoch-runter verschieben kann oder in der Breite verändert.
• Beispiele mit Gleichungen und Graphen zu Parabeln, die verschoben, gestreckt oder gestaucht werden.
• Aufgaben / Übungen um Parabeln zu üben.
• Ein Video zu diesem Thema.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Ihr solltet bereits wissen, was eine Gleichung ist und was ein Koordinatensystem ist. Wer davon noch keine Ahnung hat sieht bitte erst in Gleichungen lösen und x-y-Koordinatensystem rein.

Parabel: Normalparabel und Verschiebung

Sehen wir uns erst einmal an, was eine Parabel ist:

Je nachdem wie groß a ist, sieht die Parabel anders aus.

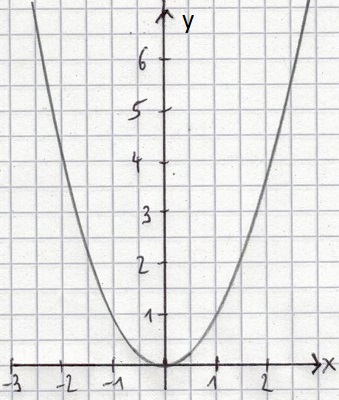
Beispiel 1: Normalparabel

Welche Eigenschaften hat eine Normalparabel und wie sieht diese aus?

Lösung:

Für a = 1 erhalten wir wie bereits in der Infobox erklärt eine Normalparabel. Die Gleichung der Normalparabel lautet damit y = x². Die nächste Grafik zeigt das Aussehen einer Normalparabel.

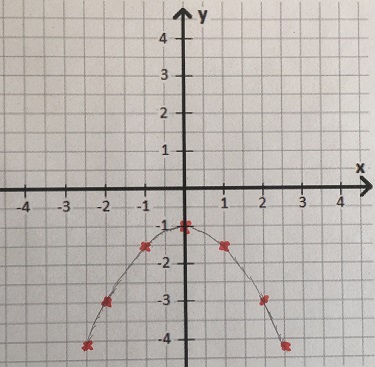
Beispiel 2: Parabel verschieben

Wir haben eine verschobene Parabel mit dieser Funktion:

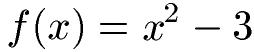
Lege eine Wertetabelle an und zeichne mit dieser den Funktionsgraphen der Gleichung.

Lösung:

Wir setzen in die Funktion für x Zahlen ein. Tun wir dies, erhalten wir Zahlen für f(x). Um die Wertetabelle auszufüllen, setzen wir für x die Zahlen 0, 1, 2, -1 und -2 ein. Damit berechnen wir die Zahlen für f(x).

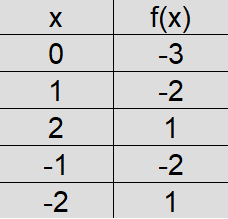
Wir nehmen ein leereres Koordinatensystem und zeichnen die Punkte aus der Wertetabelle ein. Dazu machen wir zum Beispiel bei x = 0 und f(x) = -3 ein kleines grünes Kreuzchen. Dies machen wir für alle Punkte und verbinden diese im Anschluss.

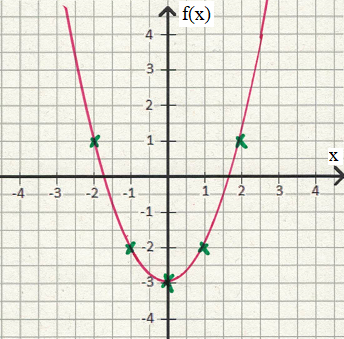
Wem diese paar Punkte nicht reichen zum Zeichnen der Parabel, der setzt noch mehr x-Werte ein um Punkte zu berechnen, zum Beispiel x = 1,5 oder x = 2,5 oder auch x = 0,5.

Anzeige:

Parabel stauchen und strecken

Parabeln können auch schmaler sein als eine Normalparabel oder eben auch breiter. Beide Fälle sehen wir uns hier einmal an.

Beispiel 3: Parabel breiter (gestaucht)

Wir haben eine Parabel mit der folgenden Gleichung. Lege eine Wertetabelle an, fülle diese aus und zeichne diese in ein Koordinatensystem. Wie sieht die Parabel aus?

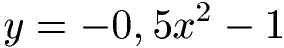
Lösung:

Wir setzen für x verschiedene Zahlen ein und berechnen damit y. Dies tragen wir in die Wertetabelle ein.

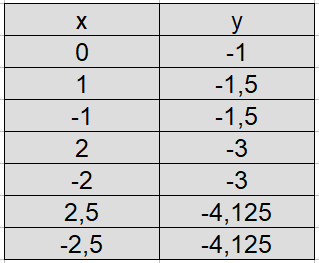
Diese x-y-Punkte tragen wir in ein Koordinatensystem ein und verbinden diese Punkte. Dabei kann man erkennen, dass diese Parabel breiter (gestaucht) ist als eine Normalparabel. Wegen dem Minuszeichen vor 0,5 ist die Parabel nach unten geöffnet.

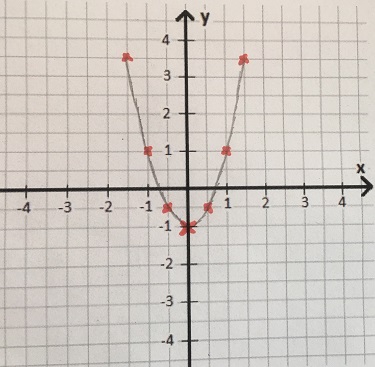
Beispiel 4: Parabel schmaler (gestreckt)

Wir haben eine Parabel mit der folgenden Funktion. Lege eine Wertetabelle an, fülle diese aus und zeichne diese in ein Koordinatensystem. Wie sieht die Parabel aus?

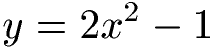
Lösung.

Auch bei dieser Aufgabe setzen wir für x verschiedene Zahlen ein und berechnen damit y. Diese Punkte tragen wir in die Wertetabelle ein.

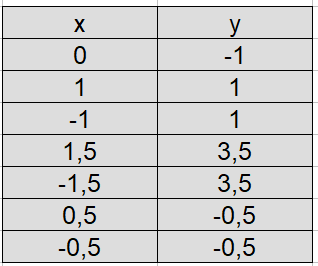
Wir nehmen erneut ein leeres Koordinatensystem und zeichnen die Punkte aus der Wertetabell ein. Diese verbinden wir und sehen, dass die Parabel schmaler (gestreckt) ist als eine Normalparabel.

Video Parabel

Anzeigen:

Fragen mit Antworten Parabel verschieben, stauchen und strecken