Parabel (Mathe) mit Formel / Gleichung

Was eine Parabel ist und wie man sie beschreibt, lernt ihr hier. Zum Inhalt:

• Eine Erklärung, wie eine Parabel aussieht und wie man sie mit Formel / Gleichung beschreibt.
• Beispiele zur Parabel.
• Aufgaben / Übungen um Parabeln zu üben
• Ein Video diesem Thema.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Ihr solltet bereits wissen was eine Gleichung ist und was ein Koordinatensystem ist. Wer davon noch keine Ahnung hat sieht bitte in Gleichungen lösen und x-y-Koordinatensystem rein.

Parabel: Erklärung und Definition

Was ist eine Parabel?

Je nachdem wie groß a ist, sieht die Parabel etwas verschieden aus. Für a = 1 erhalten wir wie bereits in der Infobox erklärt eine Normalparabel. Zeichnet man diese erhält man solch einen Graphen:

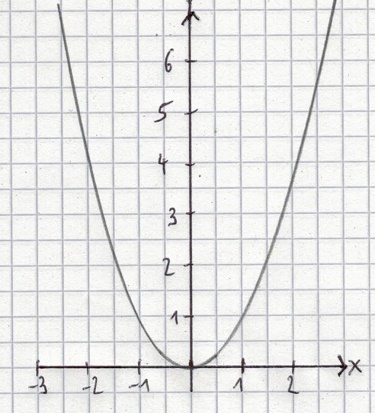
Was kann man mit einer Parabel machen?

• Parabel zeichnen: Zunächst einmal kann man eine Parabel zeichnen. Man legt dazu meistens ein Koordinatensystem und eine Wertetabelle an. In die Funktion bzw. Gleichung der Parabel werden Zahlen eingesetzt um damit die Wertetabelle auszufüllen. Im Anschluss kann man damit den Graphen der Parabel zeichnen. Wie dies funktioniert lernt ihr unter Parabel zeichnen mit Wertetabelle.
• Parabel verändern: Weiter oben hatten wir die Normalparabel. Parabeln können jedoch ganz verschieden aussehen. Sie können breiter oder schmaler sein als die Normalparabel. Die Parabel kann auch in eine andere Richtung geöffnet sein oder sie wurde nach oben oder unten verschoben. Dies sehen wir uns an unter Parabel verschieben, stauchen, strecken.
• Quadratische Funktion: Eine Parabel ist eine spezielle Form einer quadratischen Funktion bzw. quadratischen Gleichung. Wer dazu mehr erfahren möchte sieht in Quadratische Funktion lösen rein.
• Scheitelpunkt: Wie man den Scheitelpunkt berechnet bzw. was die Scheitelpunktform und auch die Produktform sind, lernt ihr unter Scheitelpunkt / Produktfom.

Anzeige:

Beispiele Parabel

In diesem Abschnitt sehen wir uns noch ein paar Beispiele zum Rechnen bei einer Parabel an.

Beispiel 1: Punkt auf Parabel

Wie haben einen Punkt P mit x = -1 und y = 4. Wie groß ist a bei der Funktionsgleichung der Parabel? Ist dies eine Normalparabel?

Lösung:

Wie haben die allgemeine Gleichung einer Parabeln mit y = ax². Wir setzen in diese x = -1 ein und y = 4. Damit berechnen wir a.

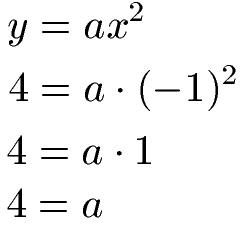
Wir berechnen damit a = 4. Da dieses a nicht 1 ist, haben wir keine Normalparabel.

Beispiel 2: Punkt auf Normalparabel

Wir haben eine Normalparabel und x sei 3. Wie groß ist y?

Lösung:

Eine Normalparabel hat die Funktion y = x². Wir setzen hier x = 3 ein und berechnen damit y.

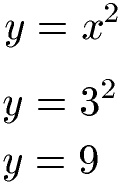
Ist bei der Normalparabel x = 3 dann erhalten wir y = 9.

Aufgaben / Übungen Parabel

Aufgabe 1: Was macht eine Parabel zu einer Normalparabel?

• a = 0
• a = 2
• a = 1
• a = 3

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Parabel

Fragen mit Antworten Mathe-Parabel