Fläche unter Kurve / Funktion berechnen

Mit der Fläche unter oder über einer Funktion / Kurve befassen wir uns hier. Dies sehen wir uns an:

• Eine Erklärung, was die Fläche unter einer Funktion ist.
• Beispiele für die Flächenberechnung.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur Flächenberechnung mit Integralen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Ihr solltet bereits wissen was die Integration in Mathe überhaupt bedeutet. Wer davon noch keine Ahnung hat, wirft bitte erst einmal einen Blick in die Grundlagen der Integration.

Fläche unter Funktion Erklärung

Mit der Integralrechnung kann man die Fläche unter einer Funktion berechnen. Dazu muss man die Funktion kennen sowie den Bereich für welche die Fläche berechnet werden soll.

Beispiel 1: Einführendes Beispiel

Für die Funktion y = f(x) = 2x soll die Fläche zwischen Funktion und x-Achse berechnet werden. Dies soll zwischen x = 0 und x = 2 passieren.

Lösung:

Um die Aufgabenstellung zu verstehen zeichnen wir die Funktion erst einmal in ein Koordinatensystem ein. In grün wird die Fläche markiert zwischen x = 0 und x = 2 unter der Funktion bis zur x-Achse hin. Diese Fläche soll berechnet werden.

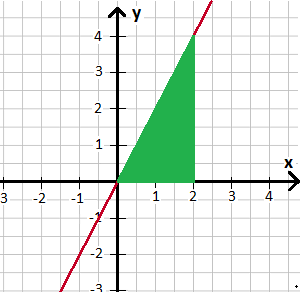
Um die Fläche unter der Kurve mit einem Integral zu berechnen müssen wir f(x) = 2x nach x integrieren (daher das dx dahinter). Die untere Grenze ist 0 und die obere Grenze ist 2. Damit sieht das zu lösende bestimme Integral so aus:

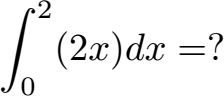
Mit der Potenzregel der Integration integrieren wir 2x und erhalten x². Die Grenzen bleiben bei 0 und 2 und werden hinter die eckige Klammer geschrieben. Im Anschluss setzen wir die obere Grenze mit x = 2 ein und wir erhalten 2². Dahinter ein Minuszeichen gefolgt vom Einsetzen der unteren Grenze mit x = 0 was uns 0² bringt. Wir erhalten als Ergebnis eine Fläche von 4.

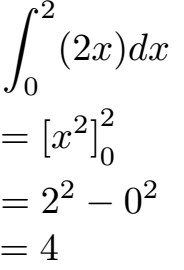
Anzeige:

Fläche berechnen über Funktion

In diesem Abschnitt sehen wir uns das "Problem mit negativen Flächen" an.

Beispiel 2: Fläche berechnen

Die Funktion f(x) = x² - 3 und die x-Achse begrenzen eine Fläche vollständig. Wie groß ist diese Fläche?

Lösung:

Wir zeichnen zunächst einmal die Funktion in ein Koordinatensystem. Dadurch sehen wir die Fläche, welche gemeint ist.

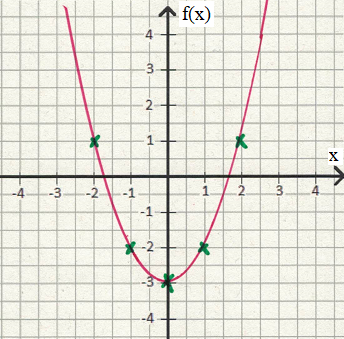
Wie man sehen kann haben wir eine Parabel mit der Spitze unter der x-Achse. Es entsteht dabei eine Fläche, die bei f(x) = -3 nach unten hin endet. Nach oben hin wird die Fläche breiter und Irgendwo so bei x = 1,7 und x = -1,7 endet die Fläche zur Seite hin. Dies sind die Schnittpunkte mit der x-Achse. Rechnerisch erhalten wir diese durch y = 0.

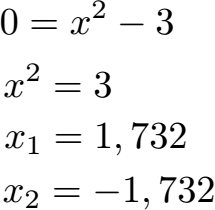
Man nennt dies die Berechnung von Nullstellen. Wir erhalten diese bei x₁ = 1,732 und x₂ = -1,732. Dies sind auch die Grenzen für unsere Integration. Wir berechnen die Fläche für f(x) = x² - 3 und diesen beiden Schnittpunkten. Die kleine Zahl ist dabei die untere Integrationsgrenze, die größere Zahl die obere Integrationsgrenze.

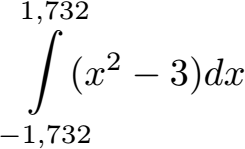
Dieses bestimmte Integral müssen wir jetzt lösen. Dazu verwenden wir die Potenzregel und die Summenregel. Wer diese beiden Regeln nicht kennt wirft bitte einen Blick auf die Integrationsregeln. Integrieren wir x² - 3 erhalten wir x³ : 3 - 3x. Die Grenzen bleiben erhalten und werden im nächsten Schritt eingesetzt. Zunächst setzen wir die obere Grenze 1,732 ein. Danach setzen wir -1,732 ein für x. Zwischen beides kommt ein Minuszeichen:

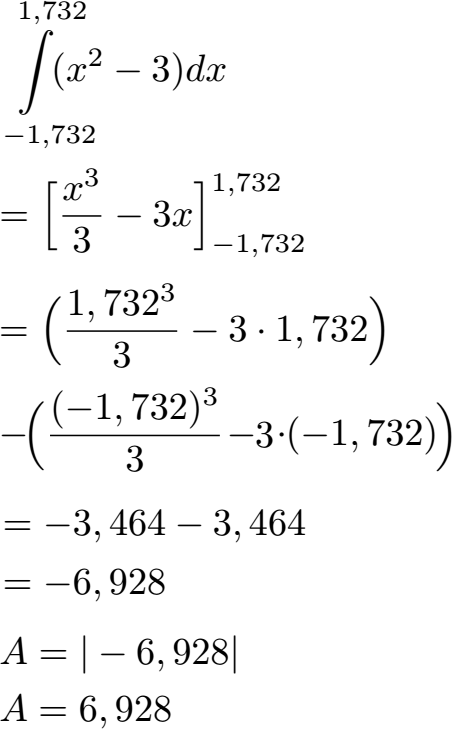
Wir erhalten als Ergebnis -6,928. Eine negative Fläche gibt es natürlich nicht. Das Minuszeichen sagt aus, dass die Fläche unter der x-Achse liegt. Wir bilden daher den Betrag und erhalten A = 6,928. Da wird die Einheit nicht kennen, es sich aber um eine Fläche handelt schreibt man manchmal dafür auch A = 6,928 FE mit FE für Flächeneinheiten.

Video Integralrechnung und Fläche

Anzeigen:

Fragen mit Antworten Fläche unter Funktion