Partielle Integration / Produktintegration

Wie man die partielle Integration (Produktintegration) anwendet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, wofür man die partielle Integration benutzt.
• Beispiele für den Einsatz dieser Integrationsregel.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur partiellen Integration.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Die partielle Integration ist die Umkehrung der Produktregel. Es macht daher Sinn, wenn ihr diese bereits kennt. Es hilft außerdem wenn ihr die Potenzregel der Integration kennen.

Partielle Integration Formel und Erklärung

Es gibt verschiedene Regeln um Funktion zu integrieren. Eine Regel davon wird als partielle Integration oder auch als Produktintegration bezeichnet.

Zum Beispiel diese Funktionen können mit der partiellen Integration integriert werden:

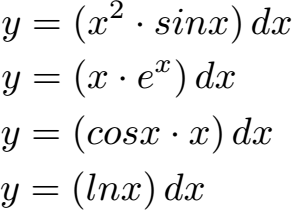
Das dx besagt, dass nach x integriert werden soll. Weiter unten sehen wir uns Beispiele zur Produktintegration an. Zunächst jedoch die allgemeine Formel.

Partielle Integration Formel:

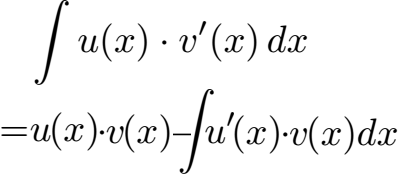
Tipps zur Produktintegration:

• Das Produkt muss so in u(x) und v'(x) zerlegt werden, dass für v'(x) eine einfache Integration möglich ist. Gelingt dies nicht sollte u(x) und v'(x) vertauscht werden.
• Das Integral u'(x) · v(x) dx muss elementar lösbar sein.

Sehen wir uns einige Beispiele zur Produktintegration an.

Anzeige:

Partielle Integration Beispiele

In diesem Abschnitt sehen wir uns Beispiele zur partiellen Integration an.

Beispiel 1: Einfache partielle Integration

Wie lautet die Stammfunktion der folgenden Funktion?

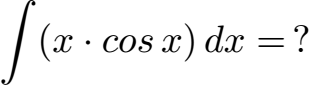
Lösung:

Wir müssen zunächst u und v' festlegen. Wir versuchen es dabei mit u = x und v' = cos x. Im nächsten Schritt leiten wir u = x ab und erhalten u' = 1. Wir integrieren v' = cos x und erhalten v = sin x.

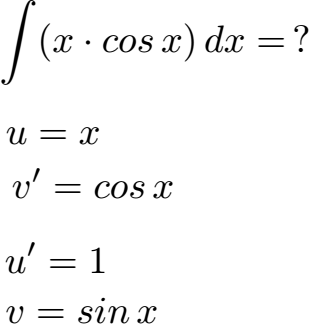
Um die Integration durchzuführen, nehmen wir die Formel der partiellen Integration. Diese wird in der vereinfachten Form hier angegeben. Im nächsten Schritt setzen wir u, u', v und v' ein. Hinter dem Integralzeichen können wir 1 · sin x zu sin x vereinfachen. Integriert man sin x wird daraus -cos x. Außerdem ergänzen wir die Konstante + C. Im letzten Schritt vereinfachen wir noch ein wenig.

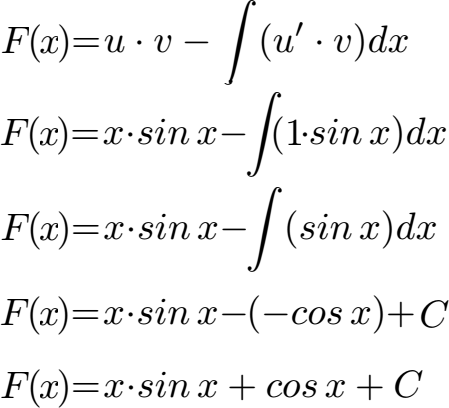
Beispiel 2: Doppelte partielle Integration bei E-Funktion mit Grenzen

In diesem Beispiel soll eine etwas kompliziertere Aufgabe behandelt werden. Bei dieser muss eine doppelte / mehrfache partielle Integration durchgeführt werden. Es ist eine E-Funktion zu beachten bei der Integration und die Funktion weist Grenzen auf. Dies ist die Aufgabe:

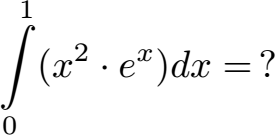
Lösung:

Wir legen zunächst u und v' fest. Durch Ableitung von u erhalten wir noch u', durch Integration von v' erhalten wir v. Im Anschluss nehmen wir die allgemeine Formel der partiellen Integration

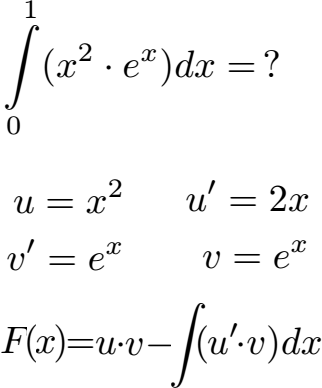
In die allgemeine Formel der partiellen Integration setzen wir u, v, u' und v' ein. Die Grenzen 0 und 1 beim Integral lassen wir erst einmal weg, diese benötigen wir erst später.

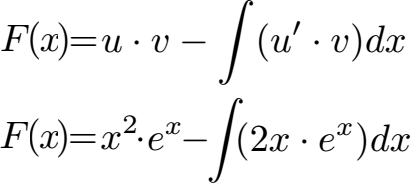
Jetzt erkennt man, dass die partielle Integration doppelt anwendet werden muss. Hinter dem Integral haben wir kein Grundintegral / Stammintegral, welches wir direkt lösen könnten. Daher müssen wir die partielle Integration mehrfach anwenden. Um dies zu tun, bleibt der Ausdruck x² · e^x vor dem Integral erhalten. Auf den Rest dahinter wenden wir wieder die partielle Integration an. Dazu legen wir erneut u und v' fest und bilden u' und v. Dabei entsteht mit 2e^x ein Integral, welches sich direkt lösen lässt.

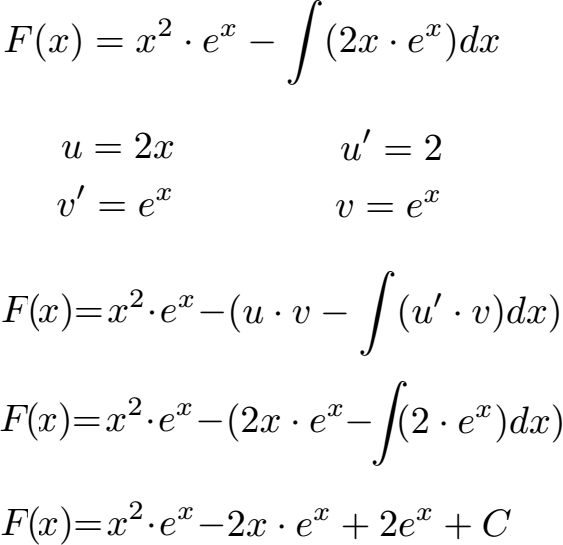
Wir kennen nun die Stammfunktion F(x). Fehlt uns noch der Einsatz der Grenzen. Dazu setzen wir x = 1 in den Ausdruck ein und ziehen davon den Ausdruck ab wenn x = 0 eingesetzt wurde. Dies rechnen wir aus und erhalten etwa 0,72.

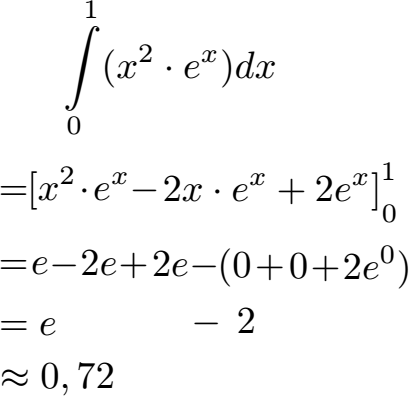
Aufgaben / Übungen Produktintegration

Aufgabe 1:

• Wie lautet die Lösung dieser Aufgabe?

Hinweis:

• Zur Lösung der Aufgabe wird die partielle Integration benötigt.
• Ich empfehle ein Blatt Papier neben dem PC um die Aufgaben zu lösen.

• F(x) = 2xe^x - e^x + C
• F(x) = xe^x - e^2x + C
• F(x) = xe^x - e^x + C
• F(x) = e^x - e^x + C

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 2 Aufgaben erfolgreich gelöst.

Anzeigen:

Video partielle Integration

Fragen mit Antworten zur partiellen Integration