Integral berechnen und Bedeutung

Wie man ein Integral berechnet und was dies bedeutet, erklären wir euch hier. Dies sehen wir uns an:

• Eine Erklärung, wie man ein Integral berechnet.
• Beispiele für das Lösen von Integralen.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur Integralrechnung.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns hier durchaus die Grundlagen der Integralrechnung an. Wem dies jedoch noch nicht ausführlich genug ist wirft bitte noch einen Blick in die Grundlagen der Integration. Ansonsten sehen wir uns nun an wie man unbestimmte Integrale und bestimmte Integrale berechnet.

Unbestimmtes Integral berechnen

Eine wichtige Grundlage der Integralrechnung besteht darin unbestimmte Integrale lösen zu können. Dabei hat man eine Funktion f(x) und soll diese integrieren. Integrieren ist das Gegenteil von Ableiten.

Beispiel 1: Unbestimmtes Integral lösen

Beginnen wir mit einem einfachen Beispiel. Es soll f(x) = 2x integriert werden.

Lösung:

Wir verwenden das Integralzeichen und schreiben dahinter 2x. Integriert werden soll nach x, daher schreiben wir dx dahinter. Was ergibt dies? Um Integrationsaufgaben zu lösen wendet man Integrationsregeln an. Weiter unten beschäftigen wir uns mit diesen Regeln. Für hier ist zunächst wichtig, dass man die Stammfunktion mit F(x) bezeichnet. Diese ist praktisch das Ergebnis der Integration.

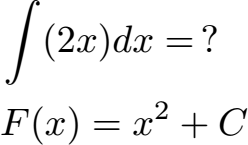
Regeln Integrale:

Es gibt verschiedene Integrationsregeln um Funktionen zu integrieren. Um diesen Artikel nicht extrem in die Länge zu ziehen, wird die Regel mit einem Beispiel kurz vorgestellt. Wenn ihr die entsprechende Regel lernen wollt findet ihr darunter den Link zum Thema.

Potenzregel: Eine Potenz wie zum Beispiel f(x) = x³ wird mit der Potenzregel integriert. Wie diese Regel funktioniert und weitere Beispiele findet ihr unter Potenzregel der Integration.

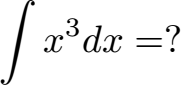
Faktorregel: Ein konstanter Faktor darf vor das Integral gezogen werden wie zum Beispiel die 3 im nächsten Beispiel. Mehr zu dieser Regel findet ihr unter Faktorregel der Integration.

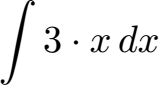
Summenregel: Summen und Differenzen werden gliedweise integriert. Im nächsten Beispiel mit f(x) = 3x + 2 ist dies der Fall. Die Summenregel (Differenzenregel) mit Beispielen besprechen wir unter Summenregel der Integration.

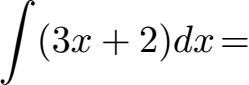
Produktintegration: Eine Funktion kann auch in Form eines Produktes vorliegen. Dabei sind sehr unterschiedliche Arten von Funktionen möglich, wie man den Beispielen entnehmen kann. Integrieren kann man solche Funktionen mit der Produktintegration / Partiellen Integration.

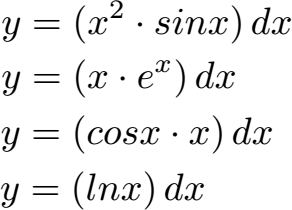
Substitution: E-Funktionen, Brüche mit Variablen im Nenner etc. müssen mit der Hilfe von Substitutionen gelöst werden. Wie dies geht lernt ihr unter Integration durch Substitution.

Anzeige:

Bestimmtes Integral berechnen

Unter Integral berechnen kann man jedoch noch etwas anderes verstehen. Bei bestimmten Integralen kann man in der Regel einen konkreten Wert berechnen. Um genau zu sein handelt es sich dabei um eine Fläche, die berechnet werden kann.

Merkt euch: Die Bedeutung vom bestimmten Integral ist eine Flächenberechnung. Ein bestimmtes Integral erkennt man daran, dass es über Integrationsgrenzen verfügt. Oben und unten am Integral steht dabei eine Zahl oder Variable.

Beispiel 1: Bestimmtes Integral berechnen

Die Fläche unter der Funktion y = 2x von x = 0 bis x = 2 soll berechnet werden. Wie groß ist die Fläche?

Lösung:

Wir müssen die Funktion f(x) = 2x nach der Variablen x integrieren (daher das dx dahinter). Das Ganze passiert daher mit der unteren Grenze 0 und der oberen Grenze 2.

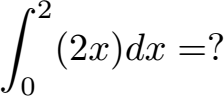
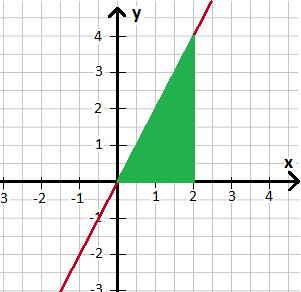
Zum besseren Verständnis noch eine Grafik, welche die zu berechnende Fläche in grün zeigt. Achtet dabei auf die Integrationsgrenzen 0 und 2.

Wie rechnet man die Fläche mit der Integralrechnung aus? Dazu integrieren wir zunächst 2x und erhalten x². Wer dies nicht versteht wirft bitte einen Blick in die Potenzregel der Integration. Die Grenzen bleiben erhalten und müssen jetzt für x eingesetzt werden. Zunächst setzen wir die obere Grenze x = 2 ein und aus x² wird 2². Danach setzen wir x = 0 ein und erhalten 0². Dazwischen ein Minuszeichen. Wir erhalten dadurch eine Fläche von 4.

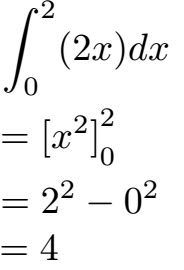
Aufgaben / Übungen Integrale berechnen

Aufgabe 1:

In diesem Bereich bieten wir euch die Möglichkeit Fragen und Aufgaben zum bestimmten Integral zu üben. Viele Schüler und Studenten scheitern jedoch schon an Begriffen und Wissen zum bestimmten Integral. Daher gibt es hier erst einmal kurz ein paar Fragen zum Thema und danach Aufgaben zum Rechnen. Wer etwas nicht mag kann auf überspringen klicken.

• Woran erkennt man ein bestimmtes Integral (im Vergleich zum unbestimmten Integral)?

• Keine Integrationsgrenzen
• Doppelintegral
• Es gibt Integrationsgrenzen
• Negative Zahlen

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Integralrechnung

Fragen mit Antworten Integral berechnen