Integrieren Grundlagen

Die Grundlagen zum Integrieren lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, wofür man das Integrieren benötigt.
• Beispiele und Erklärungen zum Integrieren von Funktionen.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zu den Grundlagen der Integralrechnung.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es ist hilfreich, wenn ihr bereits das Ableiten von Funktionen kennt. Wer davon noch nichts weiß sollte erst einmal einen Blick in die Differentialrechnung werfen.

Integration Erklärung

Was versteht man unter dem Integrieren von Funktionen und wozu benötigt man dies? Dazu erst einmal eine kleinere Erinnerung an Ableitungen. Dort hatten wir eine Funktion, die wir als f(x) bezeichneten. Mit verschiedenen Regeln wird die Funktion abgeleitet. Die 1. Ableitung wird als f'(x) bezeichnet und gibt die Steigung der Funktion an. Leiten wir erneut ab, erhalten wir die 2. Ableitung f''(x), welche das Krümmungsverhalten der Funktion angibt.

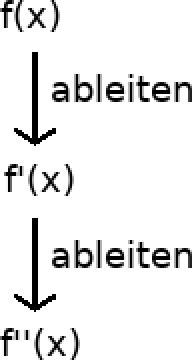
Die Berechnung kann jedoch auch in die andere Richtung durchgeführt werden. Die Umkehrung der Ableitung nennt man Integration. Hier geht man den entgegengesetzten Weg und man schließt von f''(x) auf f'(x) und weiter auf f(x).

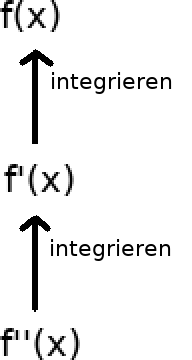
Liegt bereits f(x) vor und man integriert erneut, erhält man F(x). Leitet man hingegen F(x) wieder ab erhält man f(x).Dabei bezeichnet man F(x) als Stammfunktion von f(x).

Anzeige:

Integration Beispiele und Verwendung

Wozu braucht man die Integration? Dazu zwei kurze Beispiele zur Einleitung in das Thema:

Beispiel 1:

Von einer Bewegung wurde die Beschleunigung aufgezeichnet. Wie erhält man von dieser Bewegung die Geschwindigkeit und die Strecke?

Lösung:

• Die Beschleunigung wird in der Mathematik und in der Physik mit "a" bezeichnet.
• Integriert man die Beschleunigung erhält man die Geschwindigkeit "v".
• Integriert man die Geschwindigkeit "v" erhält man die Strecke "s".

Ausführlich vorgestellt wird diese Anwendung im Physik-Bereich.

Beispiel 2:

Eine zweite Anwendung für das Integrieren soll hier noch gezeigt werden. Durch die Integralrechnung ist es möglich die Fläche zu berechnen, die von zwei Funktionen eingeschlossen wird. Die nächste Grafik zeigt den Verlauf der Funktionen f(x) und g(x), welche eine grüne Fläche begrenzen.

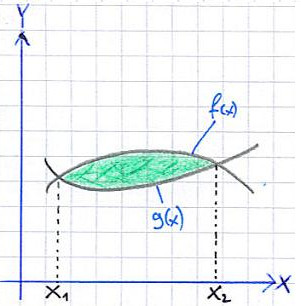
Aufgaben / Übungen Integrieren

Aufgabe 1: Bevor ihr euch an Rechenaufgaben zum Integrieren macht, solltet ihr eine Reihe an wichtigen Dingen erst einmal wissen. Genau hier könnt ihr euch mit unserem Test einmal selbst herausfordern.

• Integriere ich f(x) erhalte ich was?

• f'(x)
• f''(x)
• f(x)
• F(x)

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Integrieren Grundlagen

Fragen mit Antworten zum Integrieren