Normalform Mathe

Mit der Normalform von Funktionen und Gleichungen befassen wir uns hier. Folgende Inhalte werden angeboten:

• Eine Definition / Erklärung, wie die Normalform aussieht.
• Beispiele wie man auf die Normalform umformt.
• Übungen damit ihr dies selbst üben könnt.
• Ein Video zu quadratischen Funktionen / PQ-Formel.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns hier verschiedene Arten von Funktion bzw. Gleichungen an. Dies könnt ihr auch einzeln nachlesen unter lineare Gleichungen, quadratische Gleichung oder kubische Gleichungen (besprochen unter Polynomdivision). Ansonsten werft einfach einen Blick auf die weiteren Inhalte.

Normalform lineare Gleichung / Funktion

Was versteht man unter der Normalform?

Starten wir mit der Normalform für lineare Gleichungen bzw. lineare Funktionen.

Normalform lineare Gleichung / lineare Funktion:

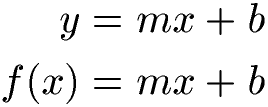
Beispiel Normalform lineare Gleichung:

Wir haben eine lineare Gleichung in der Form 4 - 2y - 8x = 0. Wie lautet diese Gleichung in Normalform dargestellt?

Lösung:

Wir führen eine Äquivalenzumformung für die Gleichung durch. Zunächst bringen wir die 4 auf die andere Seite der Gleichung, im Anschluss die -8x. Wie multiplizieren beide Seiten der Gleichung mit -1 und teilen noch durch 2. Dadurch erhalten wir die Normalform der linearen Gleichung mit y = -4x + 2.

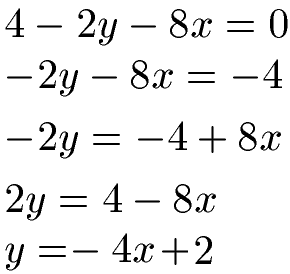
Im nächsten Abschnitt sehen wir uns die Normalformen für quadratische Funktionen und kubische Funktionen an.

Anzeige:

Normalform quadratische und kubische Funktion

Sehen wir uns als nächstes die Normalform für eine quadratische Gleichung an.

Normalform quadratische Gleichung / quadratische Funktion:

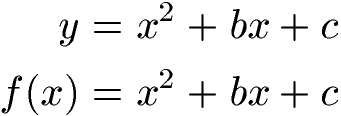
Beispiel Normalform quadratische Gleichung:

Wir haben eine quadratische Funktion, bei der eine Linearfaktorzerlegung durchgeführt wurde. Die Funktion lautet f(x) = 3(x + 1)(x - 2). Wie lautet diese quadratische Gleichung in Normalform dargestellt?

Lösung:

Wir multiplizieren zunächst die beiden Klammern aus. Jedes Element der ersten Klammer wird mit jedem Element der zweiten Klammer multipliziert. Im Anschluss wird die verbleibende Klammer mit der 3 davor multipliziert.

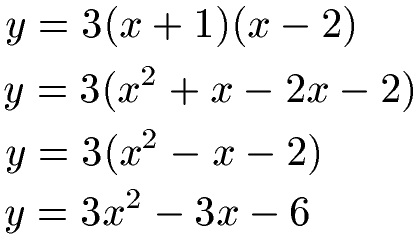
Normalform kubische Gleichung / kubische Funktion:

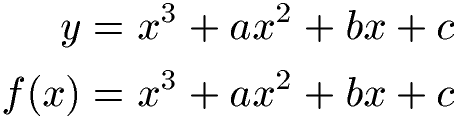
Beispiel Normalform kubische Gleichung:

Wir haben die kubische Funktion f(x) = (x + 2)(x - 1)(x + 3). Dabei handelt es sich um eine kubische Funktion 3. Grades in Linearfaktorzerlegung. Wie lautet diese Funktion in Normalform?

Lösung:

Wir multiplizieren zunächst die beiden ersten Klammern miteinander. Das Ergebnis kommt wieder in eine Klammer. Die neue große Klammer wird mit (x + 3) multipliziert und wir erhalten die Normalform der kubischen Funktion.

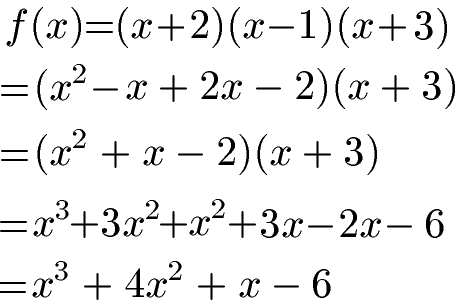
Normalform Aufgaben / Übungen

Aufgabe 1:

Wir haben die folgende Funktion:

• 4 - 2y - 8x = 0.

Wie lautet diese Funktion in Normalform dargestellt?

• y = 8x -9
• y = -4x + 2
• y = x - 2
• y = 3x + 2

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video quadratische Funktionen