PQ-Formel ohne p / ohne q

Wie kann man die PQ-Formel anwenden, wenn es kein p oder q gibt? Genau dies sehen wir uns in den nächsten Abschnitten an. Folgende Inhalte werden angeboten:

• Eine Erklärung, wie man die PQ-Formel anwendet.
• Beispiele für quadratische Gleichungen ohne p oder ohne q.
• Übungen damit ihr dies alles selbst üben könnt.
• Ein Video zur PQ-Formel.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns gleich die PQ-Formel ohne p oder q an. Falls ihr Probleme beim Verständnis bekommt, dann werft doch noch einen Blick auf den Hauptartikel PQ-Formel und quadratische Funktion lösen. Ansonsten gleich ran an die Beispiele und Lösungsformel.

PQ-Formel ohne p Beispiel

Beginnen wir mit einem Beispiel zur PQ-Formel ohne p. Zur Erinnerung noch einmal eine quadratische Gleichung und die Formel mit der man diese löst.

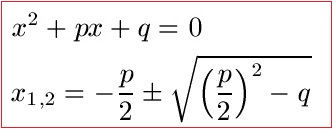
Beispiel 1: PQ-Formel ohne p

Berechnet werden soll die Lösung der Aufgabe 2x² -8 = 0.

Lösung:

Zunächst benötigen wir nur x² und nicht 2x². Aus diesem Grund teilen wir die Gleichung zunächst durch 2. Im Anschluss finden wir p und q raus. Ein p gibt es nicht, denn im Prinzip gibt es hier 0x, daher ist p = 0. Darüber hinaus können wir q = -4 ablesen. Beachtet das negative Vorzeichen, denn wir haben hier -4 in der Gleichung und eben nicht +4.

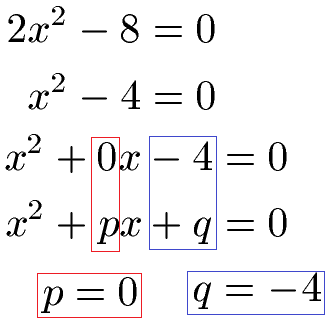
Im Anschluss nehmen wir die allgemeine Lösungsformel für die PQ-Formel und setzen dabei p und q ein. Vor der Wurzel entsteht eine 0 und unter der Wurzel eine +4. Daraus ergibt sich x₁ = 2 und x₂ = -2.

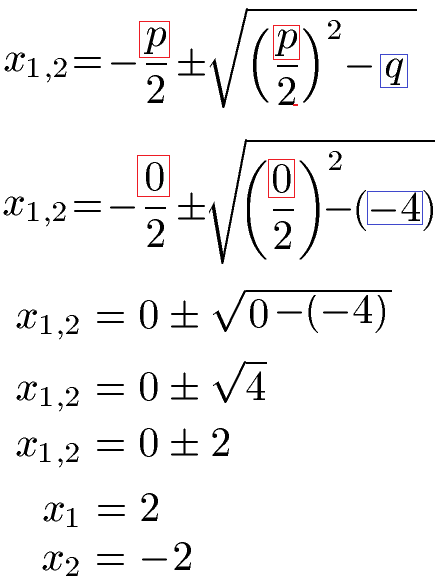
Hinweis: Es geht natürlich auch deutlich einfacher. Dazu stellen wir einfach nach x² um und ziehen schlicht und ergreifend die Wurzel.

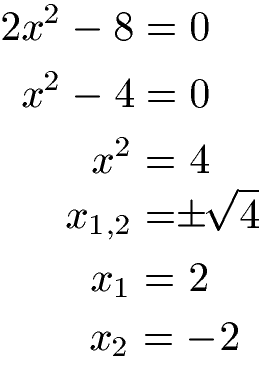
Anzeige:

PQ-Formel ohne q Beispiel

In diesem Abschnitt sehen wir uns noch die PQ-Formel ohne q an.

Beispiel 2: PQ-Formel ohne q

Löse die Aufgabe 3x² + 6x = 0 mit der PQ-Formel.

Lösung:

Wir bringen die Gleichung auf die Form mit x² am Anfang. Wir lesen p = 2 ab. Es gibt kein q, daher ist q = 0. Dies setzen wir in die allgemeine Lösungsgleichung ein und berechnen damit die beiden Lösungen für x.

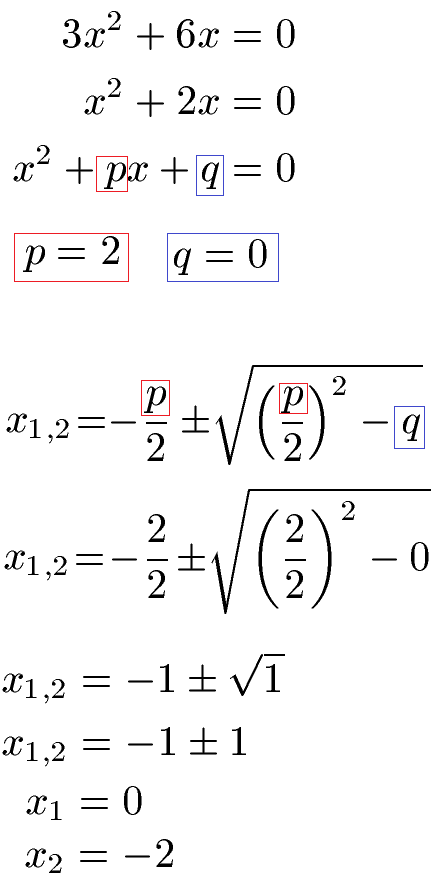
Aufgaben / Übungen PQ-Formel

Wir bieten euch im nun folgenden Aufgaben und Übungen zur PQ-Formel an. Dabei wechseln sich Aufgaben und Fagen ab. Aufgabe 1: Beginnen wir mit einer Frage. Wozu kann man die PQ-Formel verwenden?

• Zum Lösen von linearen Gleichungen
• Zum Lösen von Gleichungssystemen
• Zum Lösen von quadratischen Gleichungen
• Um Binomische Aufgaben zu lösen

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 8 Aufgaben erfolgreich gelöst.

Anzeigen:

PQ-Formel Video

Fragen mit Antworten PQ-Formel ohne p oder q