Trapez berechnen: Formeln und Eigenschaften

Die Formeln und Eigenschaften von einem Trapez bekommst du hier. Dies sehen wir uns an:

• Eine Erklärung was ein Trapez ist und wie man Fläche, Umfang etc. berechnet.
• Beispiele für Trapeze und die Verwendung von Formeln.
• Aufgaben / Übungen damit du dies selbst üben kannst.
• Ein Video zum Trapez.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Du solltet bereits einfache geometrische Körper kennen und deren Umfang oder Fläche berechnen können. Wenn du davon noch keine Ahnung hast, sieh dir bitte erst Reckteck Umfang oder Reckeck Fläche an.

Trapez: Arten, Definition und Eigenschaften

Sehen wir uns kurz die Definition für ein Trapez an:

Trapeze können ganz verschieden aussehen. Oft behandelte Arten sind gleichschenklige Trapeze, rechtwinklige Trapeze oder auch überschlagene Trapeze.

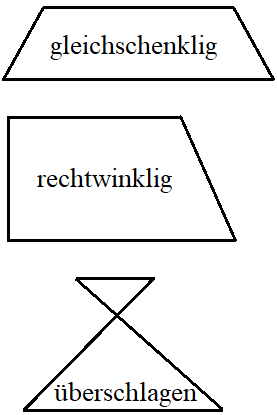
Alle Trapeze haben bestimmte gemeinsame Eigenschaften. Typische Merkmale von Trapezen sind:

• Es ist ein Viereck, hat damit 4 Ecken.
• Die Summe der Innenwinkel beträgt 360 Grad.
• Mindestens zwei Seiten sind parallel.
• Es hat 4 Seiten.
• Die parallelen Seiten sind die Grundseiten bzw. Grundlinien.
• Die beiden anderen Seiten sind die Schenkel.
• Die Mittellinie m ist in jedem Trapez parallel zu den Grundseiten.
• Die Mittellinie m ist halb so lang wie die Summe beider Grundseiten.
• Die Höhe h ist der Abstand zwischen den beiden Grundseiten.

Die Eckpunkte eines Trapezes werden mit den Buchstaben A, B, C und D bezeichnet. Die Seiten werden mit den kleinen Buchstaben a, b, c und d beschrieben. Der Abstand zwischen den parallelen Seiten ist die Höhe h. Die Mittellinie m befindet sich auf halber Höhe.

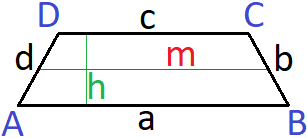
In Formeln tauchen die in der letzten Grafik dargestellten Variablen auf und ermöglichen Fläche, Umfang und andere Zusammenhänge am Trapez zu berechnen.

Anzeige:

Trapez Formeln: Flächeninhalt und Umfang

Die Formeln zum Trapez dienen dazu Flächen, Längen oder Winkel am Trapez zu berechnen. Zum besseren Verständnis werden wichtige Formeln mit Beispiel vorgerechnet.

Formel für Trapez Umfang mit Beispiel:

Die Seitenlängen von einem Trapez sind a = 10 cm, b = 3 cm, c = 8 cm und d = 3 cm. Wie lautet die Formel für den Umfang von einem Trapez und wie groß ist der Umfang von diesem Trapez?

Lösung: Den Umfang "U" von einem Trapez bekommst du durch Addition aller Seitenlängen.

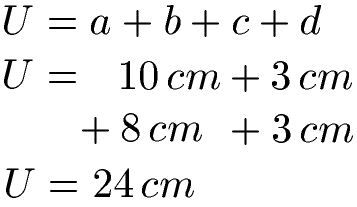
Wir erhalten einen Umfang des Trapezes von 24 Zentimetern.

Formel für Trapez Flächeninhalt (Fläche) mit Beispiel:

Gib die zwei Formeln für die Berechnung der Fläche von einem Trapez an. Berechne danach den Flächeninhalt wenn die Seite a = 10 cm ist und c = 8 cm ist. Die beiden parallelen Grundseiten sind dabei 4 cm auseinander.

Lösung: Mit a = 10 cm, c = 8 cm und h = 4 cm gehen wir in die Formeln zur Berechnung des Flächeninhaltes.

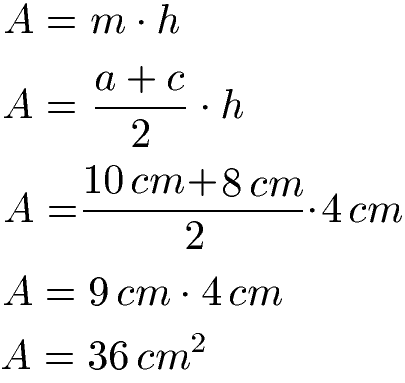
Der Flächeninhalt von diesem Trapez beträgt 36 Quadratzentimeter.

Übungen / Aufgaben Trapez

Aufgabe 1: Bevor wir rechnen ein paar Fragen. Die erste Frage ist schon einmal einfach: Wie viele Ecken hat ein Trapez?

• 4
• 2
• 3
• 1

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 6 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Trapez

Fragen mit Antworten Trapez