Irrationale Zahlen

Was irrationale Zahlen sind, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung was irrationale Zahlen sind.
• Beispiele für irrationale Zahlen.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zu Zahlenarten.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Wir sehen uns gleich auch noch den Unterschied zwischen rationalen und irrationalen Zahlen an. Wer dennoch erst einmal die rationalen Zahlen sehen möchte, wirft erst einmal einen Blick auf den Artikel rationale Zahlen.

Erklärung irrationale Zahlen

Starten wir mit den Eigenschaften bzw. der Definition zu den irrationalen Zahlen:

Als Symbol bzw. Zeichen oder Buchstabe für die irrationalen Zahlen wird manchmal ein I mit Doppelstrich verwendet.

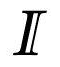
Unterschied rational und irrational:

Klären wir noch den Unterschied zwischen einer rationalen Zahl und einer irrationalen Zahl:

• Eine rationale Zahl ist eine Zahl, die durch einen Bruch dargestellt werden kann.
  • Dabei muss sowohl im Zähler als auch im Nenner eine ganze Zahl stehen.
  • Die Null im Nenner ist jedoch nicht erlaubt.
• Irrationale Zahlen sind hingegen Zahlen, die nicht als Bruch aus zwei ganzen Zahlen dargestellt werden können.

Beispiele für irrationale Zahlen sehen wir uns im nächsten Abschnitt an. Darunter fallen aber zum Beispiel:

• die Kreiszahl,
• die eulersche Zahl,
• die Wurzel aus sehr vielen Zahlen

Noch ein Hinweis: Fasst man die Mengen der rationalen und irrationalen Zahlen zusammen, erhält man die Menge der reellen Zahlen.

Anzeige:

Beispiele irrationale Zahlen

In diesem Abschnitt sehen wir uns einige Beispiele zu irrationalen Zahlen an.

Beispiel 1: irrationale Zahlen Wurzel

Die Wurzel aus Quadratzahlen sind natürliche bzw. rationale Zahlen. Alle anderen Wurzeln sind irrationale Zahlen. Grund: Zieht man die Wurzel aus diesen Zahlen entstehen Dezimalzahlen, welche nach dem Komma nicht enden und nicht periodisch sind.

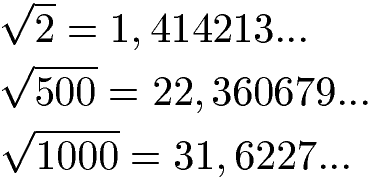
Beispiel 2: irrationale Zahl Pi

Berechnet man Fläche oder Umfang von einem Kreis, benötigt man dafür die Kreiszahl Pi. Diese Kreiszahl ist etwas größer als 3, wie ihr in der nächsten Grafik sehen könnt:

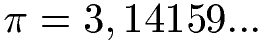
Wie man diese Kreiszahl einsetzt lernt ihr zum Beispiel unter Fläche Kreis und Umfang Kreis.

Beispiel 3: irrationale Zahl Eulersche Zahl

In Berechnungen der Naturwissenschaft und bei Ingenieuren wird sehr oft die Eulersche Zahl verwendet. Auch dabei handelt es sich um eine irrationale Zahl. Wie groß diese etwa ist sehr ihr in der nächsten Grafik:

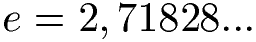
Aktuell haben wir noch keinen eigenständigen Artikel zur eulerschen Zahl. Dieser folgt später noch.

Irrationale Zahlen Aufgaben / Übungen

Aufgabe 1: Wir Wurzel aus 4 ist.... ?

• eine rationale Zahl
• eine negative Zahl
• eine irrationale Zahl
• eine periodische Zahl

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Zahlenarten

Fragen mit Antworten irrationale Zahlen