Rationale Zahlen einfach erklärt

Geschrieben von: Dennis Rudolph
Mittwoch, 13. April 2022 um 10:12 Uhr

Was rationale Zahlen sind und wie man mit diesen rechnet, lernst du hier. Dies sehen wir uns an:

Eine Erklärung was rationale Zahlen sind.
Beispiele für rationale Zahlen und wie man mit diesen rechnet.
Aufgaben / Übungen damit ihr dies selbst üben könnt.
Ein Video zu rationalen Zahlen.
Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Rationale Zahlen werden ab der 5. Klasse bis zum Abitur behandelt. Um dir den Mathematik-Unterricht zu vereinfachen, solltest zu verstehen, was eine rationale Zahl ist und wie man mit dieser rechnet. Die folgenden Inhalte erklären dir dies Schritt für Schritt.

Anzeigen:

Rationale Zahlen: Erklärung, Definition und Symbol

Starten wir mit der Definition für eine rationale Zahl:

Hinweis:
Ein Bruch mit einer ganzen Zahl im Zähler und einer ganzen Zahl im Nenner ist eine rationale Zahl. Dieser Bruch kann ausgerechnet werden und das Ergebnis ist ebenfalls eine rationale Zahl.

Zu den rationalen Zahlen gehören alle natürlichen Zahlen (1,2, 3, 4, ... ) und alle ganzen Zahlen (-3, -2, -1, 0, 1, 2, 3, ...). Brüche mit einer ganzen Zahl im Zähler und Nenner sind ebenfalls rationale Zahlen. Dezimalzahlen mit endlich vielen Stellen nach dem Komma sowie periodisch Kommazahlen gehören ebenfalls zu dieser Zahlenart. Alle Zahlen in der nächsten Grafik sind rationale Zahlen.

Beispiele rationale Zahlen:

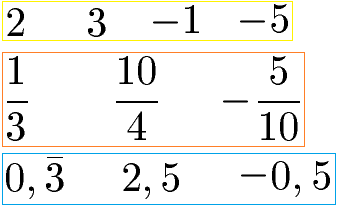
Rationale Zahlen Beispiele: Natürliche und ganze Zahlen, Brüche und Dezimalzahlen

Das Gegenteil von rationalen Zahlen sind nicht rationale Zahlen, auch irrationale Zahlen genannt. Dabei handelt es sich um Zahlen mit unendlich vielen Stellen nach dem Komma, die jedoch immer verschieden sind. Die Wurzel aus 2, die Wurzel aus (minus) 8 oder die Kreiszahl Pi haben unendlich viele Stellen nach dem Komma, die sich jedoch nicht wiederholen.

Beispiele nicht rationale Zahlen:

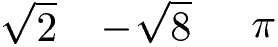
Nicht rationale Zahlen Beispiele

Das Symbol oder Zeichen für die rationalen Zahlen ist das Q:

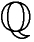
Rationale Zahlen: Zeichen und Symbol

In der Schule und im Studium wird oft mit rationalen Zahlen gerechnet. Dazu sehen wir uns jetzt die Bruchrechnung an sowie das schriftliches Rechnen für alle Grundrechenarten.

Anzeigen:

1. Rechengesetz: Kommutativgesetz für rationale Zahlen

Das Kommutativgesetz für rationale Zahlen ist gültig, egal ob es sich um Brüche oder Dezimalzahlen (Kommazahlen) bei der Berechnung handelt. Dieses Rechengesetz besagt, dass es keine Rolle spielt, in welcher Reihenfolge die Brüche oder Dezimalzahlen bei einer Addition oder einer Multiplikation stehen.

Kommutativgesetz Addition:

Im nächsten Beispiel wird die Reihenfolge der Summanden sowohl bei den Dezimalzahlen als auch bei den Brüchen vertauscht. Das Ergebnis (die Summe) ändert sich nicht.

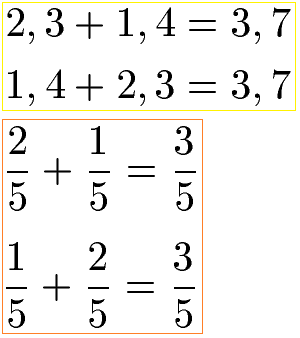
Rationale Zahlen: Kommutativgesetz für Addition

Wichtig: Solltest du die Berechnung nicht nachvollziehen können, wirf bitte für die Bruchrechnung einen Blick auf die Inhalte unter Brüche addieren und für die Dezimalzahlen auf schriftliche Addition mit Komma.

Kommutativgesetz Multiplikation:

Im nächsten Beispiel wird die Reihenfolge der Faktoren sowohl bei den Dezimalzahlen als auch bei den Brüchen vertauscht. Das Ergebnis (das Produkt) ändert sich nicht.

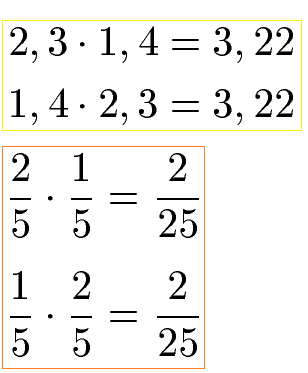
Rationale Zahlen: Kommutativgesetz der Multiplikation

Wichtig: Solltest du die Berechnung nicht nachvollziehen können, wirf bitte für die Bruchrechnung einen Blick auf die Inhalte unter Brüche multiplizieren und für die Dezimalzahlen auf schriftliche Multiplikation mit Komma.

Anzeigen:

2. Rechengesetz: Assoziativgesetz für rationale Zahlen

Das Assoziativgesetz für rationale Zahlen ist gültig, egal ob es sich um Brüche oder Dezimalzahlen (Kommazahlen) bei der Berechnung handelt. Dieses Rechengesetz besagt, dass es keine Rolle spielt, in welcher Reihenfolge drei Brüche oder drei Kommazahlen bei einer Addition oder einer Multiplikation stehen.

Assoziativgesetz Addition:

Bei der nächsten Aufgabe wird die Reihenfolge der drei Summanden sowohl bei den Kommazahlen als auch bei den Brüchen vertauscht. Das Ergebnis der Aufgabe (die Summe) ändert sich dabei nicht.

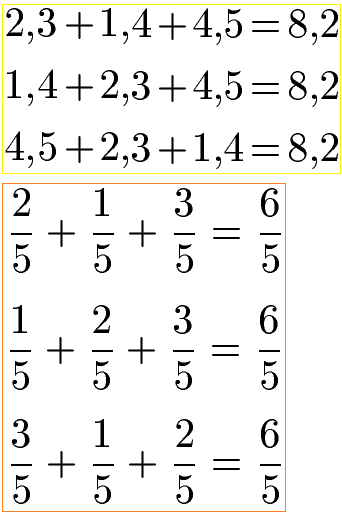
Rationale Zahlen: Assoziativgesetz der Addition

Assoziativgesetz Multiplikation:

Im nächsten Beispiel wird die Reihenfolge der drei Faktoren sowohl bei den Dezimalzahlen als auch bei den Brüchen vertauscht. Das Ergebnis (das Produkt) ändert sich nicht.

Rationale Zahlen: Assoziativgesetz der Multiplikation

Anzeigen:

3. Rechengesetz: Distributivgesetz für rationale Zahlen

Das 3. Rechengesetz ist das Distributivgesetz und kann ebenfalls für rationale Zahlen eingesetzt werden. Dieses Rechengesetz dient dazu Klammern auszumultiplizieren. Dazu wird die Zahl vor der Klammer mit jeder Zahl in der Klammer multipliziert. Solltest du die Multiplikation der Zahlen nicht im Kopf können, wirf bitte einen Blick auf die schriftliche Multiplikation mit Komma.

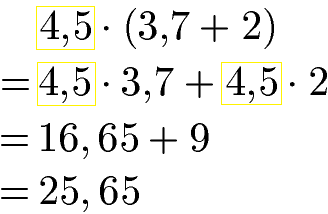
Rationale Zahlen: Distributivgesetz mit Dezimalzahlen

Das Distributivgesetz findet auch bei rationalen Zahlen in Form von Brüchen Anwendung. Dazu wird der Bruch vor der Klammer mit jedem Bruch in der Klammer multipliziert. Die Multiplikation zweier Brüche findet mit Zähler mal Zähler und Nenner mal Nenner statt. Solltest du dazu weitere Beispiele brauchen, findest du diese unter Brüche multiplizieren.

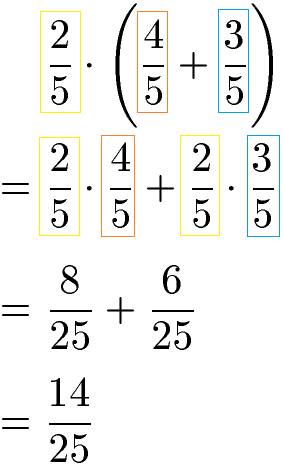
Rationale Zahlen: Distributivgesetz mit Brüchen

Brüche und Dezimalzahlen auf Zahlenstrahl (Zahlengerade)

Rationale Zahlen können auf einem Zahlenstrahl oder einer Zahlengrade eingezeichnet werden. Eine Zahlengerade ist ein Zahlenstrahl erweitert um negative Zahlen. Bei einem Zahlenstrahl oder einer Zahlengerade wird der Strahl in gleich große Abschnitte eingeteilt. Im nächsten Beispiel sind die rationalen Zahlen -0,5 und +0,75 mit einem Pfeil markiert.

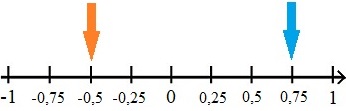
Rationale Zahlen (Zahlengerade und Zahlenstrahl) mit Dezimalzahlen

Alternativ können die Dezimalzahlen in Brüche umgerechnet werden und an den Zahlenstrahl geschrieben werden. Hier ist auf eine geeignete Einteilung zu achten. Zum Beispiel kann der Bereich zwischen 0 und 1 in vier gleich große Abschnitte unterteilt werden mit drei Strichen zwischen 0 und 1.

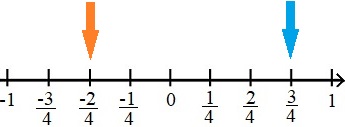
Rationale Zahlen an Zahlenstrahl (Zahlengerade) mit Brüchen

Aufgaben / Übungen rationale Zahlen

Video rationale Zahlen

Übersicht zur Zahlenart

Im nächsten Video werden die rationalen Zahlen behandelt. Du lernst dies:

Was eine rationale Zahl ist.
Ob natürliche und ganze Zahlen rational sind.
Den Unterschied zwischen rationalen und irrationalen Zahlen.
Das Rechnen mit dieser Zahlenart.

Nächstes Video »

Fragen mit Antworten zu rationalen Zahlen

In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zu rationalen Zahlen an.

Wann ist eine Zahl rational?

Eine Zahl ist rational wenn sie in Form eines Bruchs aus nur ganzen Zahlen dargestellt werden kann oder in diese Form umgerechnet werden kann.

Ist 6 eine rationale Zahl?

Ja. Die Zahl 6 kann mit dem Bruch 6 : 1 dargestellt werden. Die Zahl 6 ist eine ganze Zahl und alle ganzen Zahlen sind auch rational.

Ist 3 eine rationale Zahl?

Ja. Die Zahl 3 kann mit dem Bruch 3 : 1 dargestellt werden. Die Zahl 3 ist eine ganze Zahl und alle ganzen Zahlen sind auch rational.

Was gehört alles zu den rationalen Zahlen?

Zu den rationalen Zahlen gehören alle natürlichen Zahlen, alle ganzen Zahlen, alle Brüche mit ganzen Zahlen in Zähler und Nenner, alle Dezimalzahlen (Kommazahlen) mit einer begrenzten Anzahl an Stellen nach dem Komma und alle Dezimalzahlen mit periodischen Ziffern nach dem Komma.

Ist eine Dezimalzahl eine rationale Zahl?

Eine Dezimalzahl kann eine rationale Zahl sein, muss es jedoch nicht. Eine Dezimalzahl ist keine rationale Zahl wenn es nach dem Komma unendlich viele Stellen gibt die sich nicht wiederholen.

Was ist das Zeichen für rationale zahlen?

Das Zeichen oder Symbol für rationale Zahlen ist ein Q mit einem doppeltem Strich.

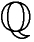
Rationale Zahlen: Zeichen und Symbol

Sind Wurzeln rationale Zahlen?

Manche Wurzeln sind rationale Zahlen, andere Wurzeln hingegen nicht. Um dies herauszufinden, muss die Wurzel gezogen werden. Entsteht beim Ziehen der Wurzel eine 1, 2, 3, 4 und so weiter als Ergebnis, ist sie rational. Entsteht hingegen eine unendlich lange Dezimalzahl ohne sich wiederholende Zahlen ist die Wurzel nicht rational.

Ist jede rationale Zahl eine ganze Zahl?
Nein. Zum Beispiel ist die rationale Zahl 3,4 keine ganze Zahl.

Wo finde ich rationale Zahlen im Alltag?

Rationale Zahlen finden sich an vielen Stellen im Alltag: So wird nur die Hälfte (0,5) einer Pizza gegessen, es ist so kalt das Wasser gefroren ist (zum Beispiel bei -4,5 Grad Celsius) oder es passen 0,75 Liter in eine Flasche.

Wie kann man rationale Zahlen darstellen?

Rationale Zahlen werden entweder als Bruch aus Zähler und Nenner oder als Dezimalzahlen (Kommazahlen) dargestellt. Sofern eine Dezimalzahl keine Stellen nach dem Komma aufweist kann diese verkürzt als natürliche Zahl (1, 2, 3, 4,...) oder ganze Zahl (..., -3, -2, -1, 0, 1, 2, 3, ...) geschrieben werden.

Ist 4:5 eine rationale Zahl?

Ja, 4:5 ist eine rationale Zahl da Zähler und Nenner des Bruchs ganze Zahlen sind.

Ist 1:3 eine rationale Zahl?
Ja, 1:3 ist eine rationale Zahl da Zähler und Nenner des Bruchs ganze Zahlen sind.

Ist 3:4 rational?

Ja, 3:4 ist eine rationale Zahl da Zähler und Nenner des Bruchs ganze Zahlen sind.

Welche Zahlen gehören zu den natürlichen Zahlen?

Zu den natürlichen Zahlen gehören 1, 2, 3, 4, 5 und so weiter. Ob die 0 zu den natürlichen Zahlen gehört ist umstritten.

Welche Zahlen gehören zu den ganzen Zahlen?
Zu den ganzen Zahlen gehören alle natürlichen Zahlen (1, 2, 3, 4, ...), sowie die natürlichen Zahlen jedoch mit einem negativen Vorzeichen (-1, -2, -3, -4 und so weiter). Die Zahl 0 zählt ebenfalls zu den ganzen Zahlen.

Sind rationale Zahlen unendlich?

Rationale Zahlen können unendlich viele Stellen nach dem Komma haben. Voraussetzung ist jedoch, dass diese in einer Periode vorkommen. Zum Beispiel 1:3 = 0,333333.... Die Zahl 3 wiederholt sich nach dem Komma immer wieder, sie ist periodisch. Daher ist 1:3 rational.

Welche Zahlen sind nicht rational?

Nicht rational sind Dezimalzahlen (Kommazahlen) mit unendlich vielen Stellen nach dem Komma, welche sich jedoch nicht wiederholen. Eine Dezimalzahl mit Periode nach dem Komma ist rational, eine Dezimalzahl mit unendlich vielen Stellen nach dem Komma ohne Periode ist nicht rational.

Sind ganze Zahlen rationale Zahlen?

Ja, alle ganzen Zahlen sind rationale Zahlen. Dies liegt daran, dass jede ganze Zahl als Bruch mit dem Nenner 1 geschrieben werden kann.

F: Welche Rechenregeln zu rationalen Zahlen muss ich beachten?

A: Rationale Zahlen sind als Bruch darstellbar. Wichtig dabei ist die Regel, dass der Nenner nicht 0 werden darf. Ansonsten gelten beim Rechnen mit rationalen Zahlen natürlich die Rechenregeln der Mathematik wie Punkt vor Strich oder Klammern zuerst.

F: Welche Inhalte sollte ich mir als nächstes ansehen?

A: Diese Inhalte zu Zahlenarten, zum Bruchrechnen und zum schriftlichen Rechnen sind bei uns verfügbar:

Anzeigen:

Neue Artikel

Hat dieser Artikel dir geholfen?