Fläche / Flächeninhalt mit Formel berechnen

Wie man Flächen berechnen kann, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung wie man die Fläche von Quadrat, Dreieck, Kreis, Trapez usw. berechnet.
• Beispiele wie man die Formeln zur Berechnung der Fläche anwendet.
• Aufgaben / Übungen damit ihr dies selbst üben könnt.
• Ein Video zum Flächeninhalt.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Ihr solltet bereits einfache Längeneinheiten kennen wie Meter oder Zentimeter und auch wissen, wie man diese ineinander umrechnet. Wer davon noch keine Ahnung hat, wirft bitte erst einmal einen Blick auf Meter, Dezimeter und Zentimeter.

Flächeninhalt berechnen: Quadrat und Dreieck

Beginnen wir mit der Fläche (Flächeninhalt) von einem Quadrat. Bei einem Quadrat sind alle vier Seiten gleich lang. In der nächsten Grafik werden diese vier Seiten daher jeweils mit a bezeichnet. Mehr wird für die Flächenberechnung gar nicht benötigt. Die Grafik erhält ergänzend noch die Bezeichnungen A bis D für die Eckpunkte und die Diagonale d.

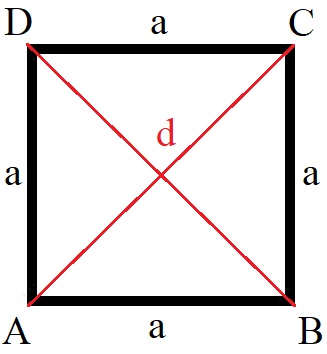
Die Fläche von einem Quadrat - mit A bezeichnet - berechnet sich mit dieser Formel:

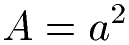
Beispiel Quadrat Fläche:

Ein Quadrat hat eine Seitenlänge von 3 Metern. Wie groß ist sein Flächeninhalt?

Lösung:

Wir setzen a = 3 m in die Formel ein. Dabei müssen wir sowohl die 3 als auch die Meter quadrieren.

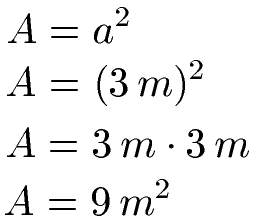
Der Flächeninhalt vom Quadrat ist 9 m² groß. Zur Fläche von einem Quadrat haben wir noch weitere Tipps und Beispiele unter Quadrat: Eigenschaften und Formeln.

Fläche (Flächeninhalt) Dreieck:

Bei der Fläche von einem Dreieck kann man zwei Fälle unterschieden. Der erste Fall ist ein Dreieck mit einem rechten Winkel und der zweite Fall ein Dreieck ohne rechten Winkel. Beginnen wir mit dem Flächeninhalt von einem Dreieck mit rechtem Winkel. Dies sieht zum Beispiel so aus:

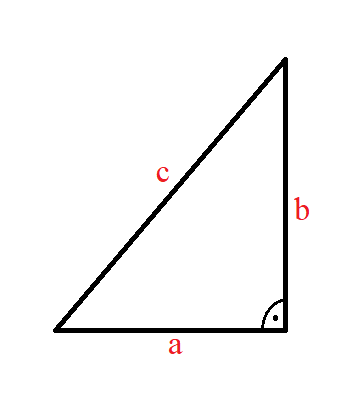
Den Flächeninhalt von diesem rechtwinkligen Dreieck berechnet man mit der Formel:

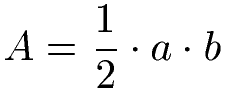
Beispiel: Fläche rechtwinkliges Dreieck

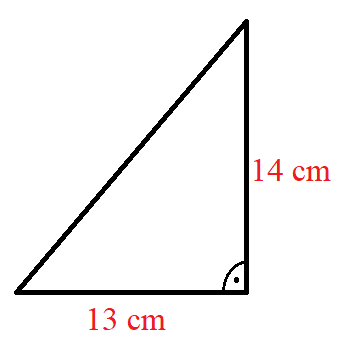
Wir haben ein Dreieck mit einem rechten Winkel in der unteren rechten Ecke. Die Katheten sind 13 cm und 14 cm lang. Wie groß ist der Flächeninhalt des Dreiecks?

Lösung:

Wir nehmen unsere Formel für die Fläche von einem rechtwinkligen Dreieck und setzen a = 13 cm und b = 14 cm ein. Wir teilen zunächst die 13 cm durch 2 und erhalten 6,5 cm. Im Anschluss multiplizieren wir 6,5 · 14 zu 91. Zu den Einheiten: Zentimeter mal Zentimeter, also cm mal cm ergibt Quadratzentimeter (cm²). Die Fläche beträgt damit 91 cm².

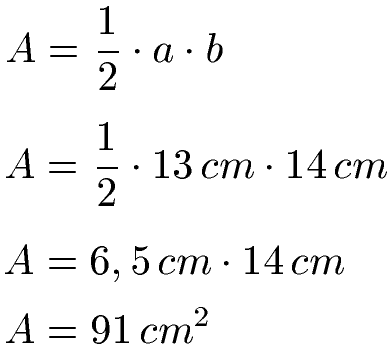
Die Fläche dieses rechtwinkligen Dreiecks liegt bei 91 cm².

Angenommen wir haben kein rechtwinkliges Dreieck, sondern ein beliebiges Dreieck. Wie berechnet man jetzt die Fläche von diesem Dreieck? Sehen wir uns dazu einmal ein solches Dreieck an, bei dem die Höhe mit eingezeichnet wurde:

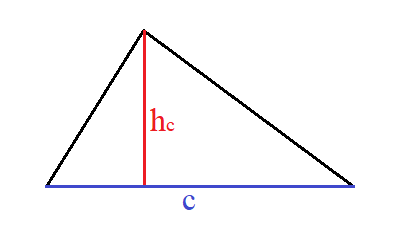
Die Seite c wird als Grundseite bezeichnet. Auf dieser Grundseite steht die Höhe h (in rot eingezeichnet). Genauer gesagt die Höhe h_c, denn so bezeichnet man die Höhe auf der Grundseite c. Diese steht im rechten Winkel auf c.

Mit der Grundseite c und der Höhe h_c kann man die Fläche des Dreiecks mit dieser Formel berechnen:

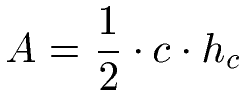
Beispiel 2: Dreieck ohne rechten Winkel

Die Grundseite eines Dreiecks sei 0,3 Meter lang und die Höhe darauf 4 cm. Wie groß ist der Flächeninhalt von diesem Dreieck?

Lösung:

Wir haben in der Aufgabenstellung verschiedene Einheiten für die Länge. Daher rechnen wir zunächst die 0,3 Meter in Zentimeter um. Im Anschluss setzen wir die 30 Zentimeter für c und die Höhe darauf mit 4 Zentimeter ein.

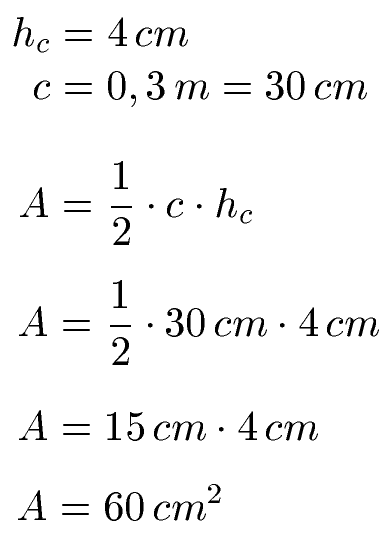
Die Fläche dieses Dreiecks liegt bei 60 cm². Mehr zu diesem Thema auch unter Fläche Dreieck berechnen.

Anzeige:

Fläche Kreis und Trapez

In diesem Abschnitt sehen wir uns die Fläche von Kreis und Trapez an. Dazu wieder eine Grafik, die Formeln bzw. Formeln und jeweils ein Beispiel.

Flächeninhalt Kreis:

Ein Kreis hat einen Radius, der von der Mitte vom Kreis bis zur Begrenzung vom Kreis geht. Der Durchmesser geht einmal durch die Mitte vom Kreis und ist doppelt so groß wie der Radius. Werft dazu einen Blick auf die Grafik.

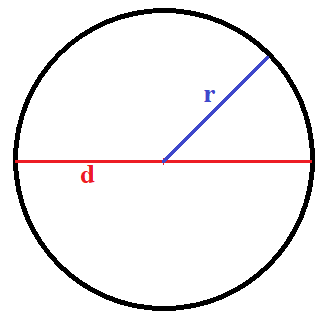
Die Fläche vom Kreis berechnet sich mit dieser Formel:

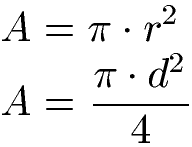
Dabei ist:

• "A" ist die Fläche von einem Kreis
• "π" ist die Kreiszahl, etwa 3,14159
• "d" ist der Durchmesser vom Kreis
• "r" ist der Radius vom Kreis

Beispiel: Fläche Kreis

Der Radius von einem Kreis sei 2,3 Zentimeter. Wie groß ist der Flächeninhalt?

Lösung:
Der Radius ist r = 2,3 cm. Dies setzen wir in die Formel mit dem Radius ein. Bei der Berechnung ist es wichtig darauf zu achten, dass nicht nur die Zahl 2,3 quadriert wird, sondern auch cm. Berechnen wir 2,3 · 2,3 erhalten wir 5,29. Aus cm · cm wird cm².

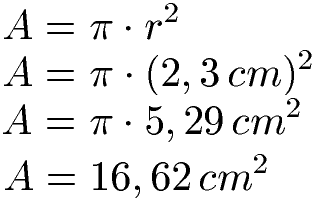
Der Kreis hat einen Flächeninhalt von 16,62 Quadratzentimeter. Mehr zum Berechnen der Fläche von einem Kreis unter Kreis Fläche / Flächeninhalt.

Trapez Fläche / Flächeninhalt:

Sehen wir uns noch die Fläche bzw. den Flächeninhalt von einem Trapez an. Dafür erst einmal eine Grafik zu einem Trapez mit entsprechenden Variablen.

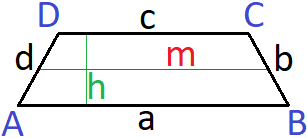
Beispiel: Trapez Fläche berechnen

Gib die zwei Formeln (Gleichungen) für die Berechnung des Flächeninhalts von einem Trapez an. Berechne danach die Fläche wenn die Seite a = 10 cm ist und c = 8 cm. Die beiden parallelen Grundseiten sind dabei 4 cm auseinander.

Lösung:

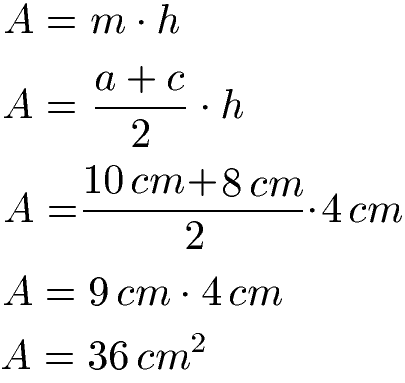
Der Flächeninhalt von diesem Trapez beträgt 36 Quadratzentimeter. Mehr zu diesem Thema auch unter Trapez: Eigenschaften und Formeln.

Aufgaben / Übungen Flächeninhalt

Aufgabe 1: Wie berechnet man die Fläche von einem Quadrat?

• A = b : 3
• A = c : 4
• A = a : 2
• A = a²

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Fläche berechnen

Fragen mit Antworten Flächeninhalt berechnen