Zinssatz berechnen (Zinszahl)

Wie man den Zinssatz bzw. die Zinszahl mit Formeln berechnet (und wo der Unterschied liegt), lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, wie man den Zinssatz (Zinszahl) für Jahre, Tage oder Monate berechnet.
• Beispiele und Formeln um den Zinssatz zu berechnen.
• Aufgaben / Übungen um dieses Thema selbst zu üben.
• Ein Video zur Zinsrechnung.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Erklärung Zinssatz / Zinszahl

Legt man Geld bei einer Bank oder in einem Finanzprodukt an, gibt es dafür oftmals Zinsen. Dadurch vermehrt sich das Geld. Wie stark die Vermehrung für einen bestimmten Geldbetrag stattfindet, hängt vom Zinssatz ab.

Unterschied Zinssatz / Zinszahl mit Beispiel:

In Formeln wird manchmal mit dem Zinssatz und manchmal mit der Zinszahl gearbeitet. Vielen ist der Unterschied zwischen Zinssatz und Zinszahl nicht klar. Der Zinssatz ist eine Angabe mit einem Prozentzeichen, die Zinszahl ist ohne Prozentzeichen. Wenn der Zinssatz 4,1 % ist, dann ist die Zinszahl 4,1. Man beachte das Prozentzeichen auf beiden Seiten beim Zinssatz in der nächsten Gleichung.

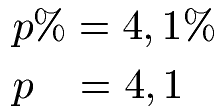
Prozent bedeutet nichts anders als Hundertstel. Damit sind 4,1 % nichts anderes als 4,1 : 100.

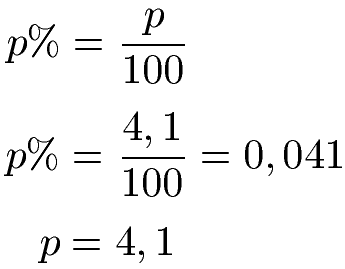
Für die Praxis merken wir uns: Der Zinssatz p % = 4,1 % entspricht der Zinszahl p = 4,1. Es ist meistens einfacher die Formel mit p anstatt p % zu nehmen, da man hier direkt rechnen kann.

Hinweis: Der Prozentsatz aus der Prozentrechnung wird in der Zinsrechnung oft als Zinssatz bezeichnet. Es handelt sich dabei jeweils um eine Angabe in Prozent.

Formel Zinssatz / Zinszahl Jahreszinsen (1 Jahr):

Wird Geld für 1 Jahr angelegt, dann kann man mit der nächsten Formel die Zinszahl bzw. den Zinssatz berechnen. Dazu nimmt man die Zinsen, welche für dieses Jahr angefallen sind und multipliziert diese mit 100. Danach wird durch das Anfangskapital dividiert:

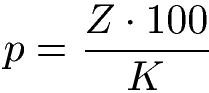
Dabei ist:

• "p" die Zinszahl
• "Z" die angefallenen Zinsen
• "K" das Anfangskapital

Von der Zinszahl p kommen wir mit einem Prozentzeichen auf den Zinssatz p%. Siehe dazu das nächste Beispiel.

Beispiel 1:

Ein Anfangskapital von 2000 Euro wirft nach einem Jahr 60 Euro Zinsen ab. Wie hoch war der Zinssatz?

Lösung:

Das Anfangskapital ist K = 2000 Euro und die Zinsen Z = 60 Euro. Dies setzen wir ein und berechnen die Zinszahl und damit den Zinssatz. Wir erhalten den Zinssatz zu p % = 3 %.

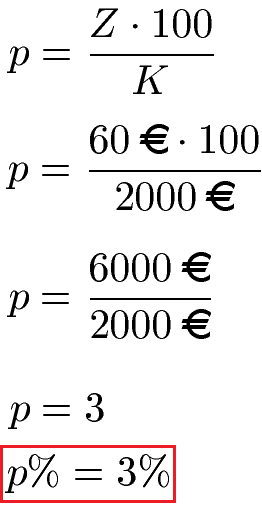
Mehr zu Jahreszinsen findet ihr unter Jahreszinsen berechnen.

Anzeige:

Beispiele und Formeln Zinssatz

Die Berechnung des Zinssatzes für 1 Jahr hatten wir im letzten Abschnitt. Als nächstes sehen wir uns die Berechnung vom Zinssatz bzw. der Zinszahl an, wenn das Geld nur einige Monate oder gar nur einige Tage angelegt wurde. Im Anschluss geht es noch um den Zinssatz für die mehrjährige Geldanlage (Zinseszins).

Formel Zinssatz / Zinszahl Monatszinsen:

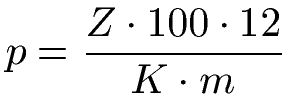
Dabei ist:

• "p" die Zinszahl
• "Z" die angefallenen Zinsen
• "K" das Anfangskapital
• "m" die Anzahl der Monate

Von der Zinszahl p kommen wir mit einem Prozentzeichen auf den Zinssatz p%. Siehe dazu das nächste Beispiel.

Beispiel 2:

Für einen Zeitraum von 3 Monaten wird eine Summe von 1450 Euro angelegt. In diesem Zeitraum entstehen 21,75 Euro an Zinsen. Wie hoch ist der Zinssatz der Anlage?

Lösung:

Die Anzahl der Monate ist m = 3. Das eingesetzte Anfangskapital K = 1450 Euro und die Zinsen Z = 21,75 Euro. Dies setzen wir in die Gleichung ein und rechnen zunächst Zähler und Nenner aus. Damit kommen wir auf die Zinszahl p = 6 und damit auf den Zinssatz p % = 6%.

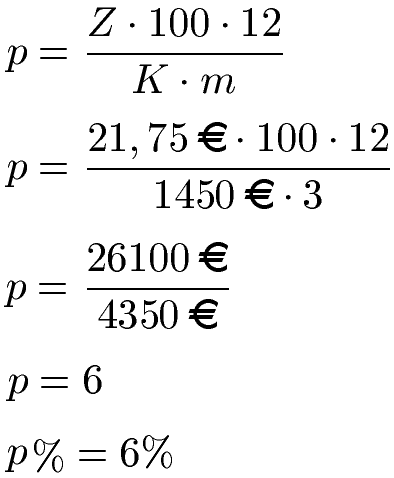
Mehr zu Monatszinsen findet ihr unter Monatszinsen berechnen.

Formel Zinssatz / Zinszahl Tageszinsen:

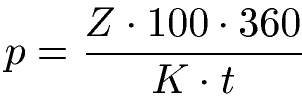
Dabei ist:

• "p" die Zinszahl
• "Z" die angefallenen Zinsen
• "K" das Anfangskapital
• "t" die Anzahl der Tage

Von der Zinszahl p kommen wir mit einem Prozentzeichen auf den Zinssatz p%. Siehe dazu das nächste Beispiel.

Beispiel 3:

Für 13 Tage wurde eine Anfangssumme von 24145 Euro angelegt und es entstanden 26,16 Euro an Zinsen. Wie hoch war der Zinssatz?

Lösung:

Der Aufgabenstellung entnehmen wir die Anzahl der Tage t = 13 sowie das Anfangskapital K = 24145 Euro und die Zinsen Z = 26,16 Euro. Wir setzen dies ein und berechnen den Zinssatz zu 3 %.

Mehr zu Tageszinsen findet ihr unter Tageszinsen berechnen.

Formel Zinssatz / Zinszahl Zinseszinsen:

Wird Geld für mehrere Jahre angelegt, dann entstehen dabei Zinseszinsen. Auch hier fragt man sich manchmal, wie hoch denn der Zinssatz war, zu dem das Geld angelegt wurde. Die Formel für die Zinszahl lautet:

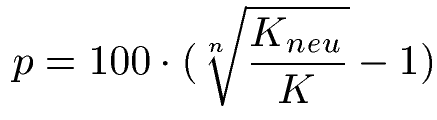
Dabei ist:

• "p" die Zinszahl
• "K_neu" das Endkapital nach Verzinsung
• "K" das Anfangskapital vor Verzinsung
• "n" die Anzahl der Jahre

Beispiel 4:

Nach 5 Jahren wurden aus 2000 Euro Anfangskapital ein Endkapital von 2102,02 Euro. Wie hoch war der Zinssatz?

Lösung:

Anfangs- und Endkapital sind bekannt sowie die Anzahl der Jahre mit n = 5. Dies setzen wir zunächst in die Gleichung ein. Zunächst rechnen wir den Bruch unter der Wurzel aus. Mit dem Taschenrechner ziehen wir die fünfte Wurzel aus 1,05101. Davon ziehen wir die 1 ab und multiplizieren im Anschluss mit 100. Die Zinszahl ist damit 1 und der Zinssatz 1%.

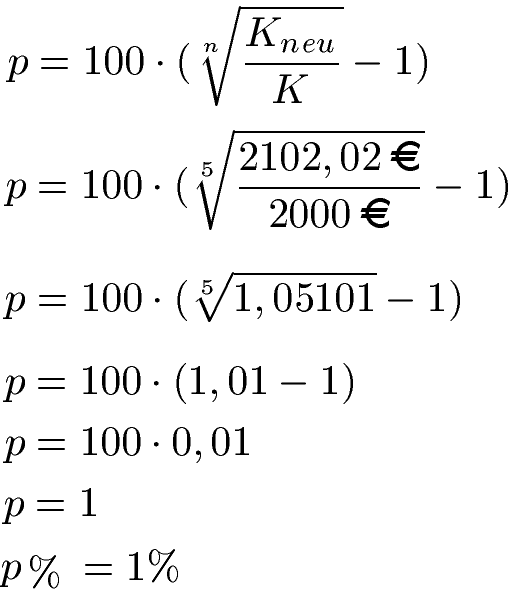
Mehr zum Zinseszins findet ihr unter Zinseszins berechnen.

Aufgaben / Übungen Zinssatz

Aufgabe 1: Bevor wir rechnen ein paar einfache Fragen zu den Formeln. Wer die Fragen nicht mag, kann auf überspringen klicken. Erste Frage: Wofür steht das p in der nächsten Formel?

• Anfangskapital
• Zinsen
• Endkapital
• Prozentzahl

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 11 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Zinssatz berechnen

Fragen mit Antworten Zinssatz