Zinsrechnung und Prozentrechnung
Geschrieben von: Dennis RudolphMontag, 22. Januar 2018 um 13:27 Uhr
Einen Überblick zur Zinsrechnung und Prozentrechnung findet ihr hier. Dies sehen wir uns an:
- Eine Erklärung, welche Themen es in der Zins- und Prozentrechnung gibt.
- Beispiele um den Zusammenhang zwischen Prozent- und Zinsrechnung zu zeigen.
- Aufgaben / Übungen um die Themen selbst zu üben.
- Videos zur Prozentrechnung und Zinsrechnung.
- Ein Frage- und Antwortbereich zu diesen Gebieten.
Wer Verständnisprobleme bei der Prozent- und Zinsrechnung bekommt, dem fehlen vielleicht ein paar wichtige Vorkenntnisse. In diesem Fall bitte in die Artikel Rechenregeln und Gleichungen auflösen reinsehen.
Erklärung Zinsrechnung und Prozentrechnung
Die Zinsrechnung ist eine Anwendung der Prozentrechnung. Aus diesem Grund wird in der Schule im Normalfall erst die Prozentrechnung besprochen und im Anschluss die Zinsrechnung.
Als nächstes seht ihr eine Übersicht an Themen. Wer sich für einen bestimmten Bereich interessiert, kann diesen gleich aufrufen. Unterhalb der Themenliste findet ihr einige leichte Erklärungen zum Einstieg. Die Liste wird ergänzt durch den Dreisatz, welcher in diesem Zusammenhang ebenfalls behandelt wird.
Prozentrechnung:
Zinsrechnung:
Dreisatz:
Ihr interessiert euch für den Zusammenhang zwischen Prozentrechnung und Zinsrechnung? Dann lest weiter. Außerdem findet ihr weiter unten noch Aufgaben / Übungen zu den Themen.
Anzeige:
Anzeigen:
Beispiele Prozent- und Zinsrechnung
Bei der Prozentrechnung geht es darum Anteile an etwas Ganzem zu berechnen. Dies drückt man in Prozent aus, zum Beispiel 5 Prozent oder 80 Prozent. In vielen Fällen ist dabei 100 % alles und 0 Prozent nichts. Die Zinsrechnung ist eine Anwendung der Prozentrechnung. Der Unterschied zwischen Prozentrechnung und Zinsrechnung liegt in erster Linie darin, dass es bei der Zinsrechnung um Geldanlagen mit Zinsen geht.
Aus diesem Grund werden bei der Zinsrechnung auch etwas andere Begriffe verwendet als bei der Prozentrechnung. So wird zum Beispiel aus dem Grundwert das Kapital. In der nächsten Tabelle findet ihr eine Übersicht der Begriffe mit den entsprechenden Abkürzungen für die Formeln.
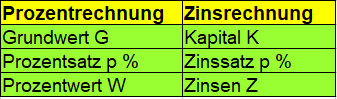
Wichtig: Das folgende Beispiel zeigt euch, wie Prozentrechnung und Zinsrechnung in einer einzigen Aufgabe vorkommen können. Daher ist diese Aufgabe auch etwas komplizierter. Ihr solltet erst die Themen weiter oben bearbeitet haben, bevor ihr euch gemischte Aufgaben wie diese anseht!
Beispiel 1:
Eine Familie hat bei einem Gewinnspiel 45000 Euro gewonnen.
a) Das Geld wird für 3 Jahre bei einem Zinssatz von 4 % angelegt. Auf welche Summe wächst der Betrag durch die Zinsen an?
b) Um wie viel Prozent ist das Kapital in den drei Jahren angewachsen?
Lösung:
Der Aufgabenstellung entnehmen wir zunächst, dass das Anfangskapital K = 45000 Euro ist.
a) Das Geld wird für mehrere Jahre angelegt und es gibt für diese Jahre Zinsen. Aus diesem Grund sind wir hier beim Zinseszins angelangt. Daher greifen wir zur Zinseszins-Formel um das Endkapital zu berechnen. Bei der Formel ist die Anlagezeit n = 3. Der Zinssatz ist p % = 4 % und damit ist das p = 4.
Wir setzen dies in die Gleichung ein. Um die Aufgabe richtig zu berechnen, müssen wir uns an die Rechenregeln halten. Diese bedeutet, dass wir zunächst die Klammer berechnen und im Anschluss die Potenz. Als Letztes wird die Multiplikation ausgeführt und ergibt ein Endkapital von Kneu = 50618,88 Euro.
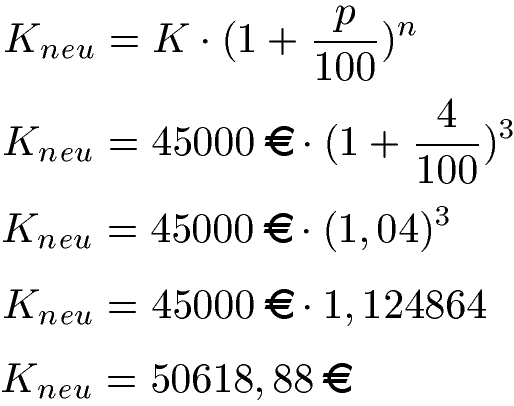
In den drei Jahren wächst das Geld auf 50618,88 Euro.
b) Im zweiten Teil der Aufgabe wurde nach dem prozentualen Anstieg des Kapitals gefragt. Hier sollte man zunächst wieder daran denken, dass das Anfangskapital bei 45000 Euro lag. Dieses Anfangskapital setzt man mit 100 % an. Jetzt wächst das Kapital auf ein Endkapital von 50618,88 Euro. Das Geld wurde mehr. Nun fragt man sich, wie viel Prozent das Endkapital sind. Dies kann man zum Beispiel so aufschreiben:
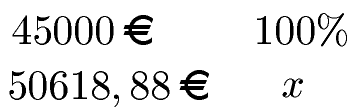
Das x soll berechnet werden. Dazu nehmen wir die 100 Prozent und multiplizieren dies mit 50618,88 Euro und dividieren durch 45000 Euro.
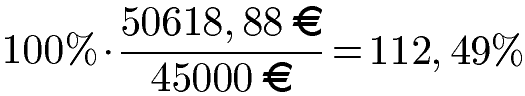
Die 50618,88 Euro entsprechenden damit 112,49 Prozent. Das Kapital ist damit um 12,49 Prozent angestiegen.
Aufgaben / Übungen
- Prozentrechnung Aufgaben / Übungen
- Dreisatz Aufgaben / Übungen
-
Zinsrechnung Aufgaben / Übungen
- Tageszinsen Aufgaben / Übungen
- Monatszinsen Aufgaben / Übungen
- Jahreszinsen Aufgaben / Übungen
- Zinsen berechnen Aufgaben / Übungen
- Kapital berechnen Aufgaben / Übungen
- Zinsfaktor Aufgaben / Übungen
- Zinseszins Aufgaben / Übungen
- Zinssatz Aufgaben / Übungen
- Zinsrechnung und Prozentrechnung Aufgaben / Übungen
- Zinsrechnung durch Dreisatz Aufgaben / Übungen
Videos Prozentrechnung und Zinsrechnung
Zinsrechnung Erklärung
Hier findet ihr noch Videos zur Zinsrechnung und Prozentrechnung. Das erste Video hier geht dabei um die Zinsrechnung. Hier werden die typischen Grundbegriffe und Formeln - auch im Vergleich zur Prozentrechnung - behandelt. Es geht um die Berechnung von Zinsen, Kapital und Zinssatz. Ihr erhaltet damit einen Überblick über das Thema. Entsprechende Beispiele mit Zahlen und Einheiten werden vorgerechnet.
Nächstes Video »
Fragen mit Antworten Prozent- und Zinsrechnung
In diesem Bereich geht es noch um typische Fragen und Antworten zur Zinsrechnung und Prozentrechnung.
F: Wann werden diese Themen in der Schule behandelt?
A: Die Prozentrechnung und Zinsrechnung wird oftmals ab der 6. Klasse behandelt. Gestartet wird dabei meistens mit den Grundbegriffen der Prozentrechnung. Spätestens in der 7. Klasse und dann auch in der 8. Klasse werden die verbleibenden Inhalte der Prozent- und Zinsrechnung behandelt. Zusätzlich werden Dreisatz und meistens auch zusammengesetzter Dreisatz besprochen.
F: Wie sieht es mit Zins- und Prozentrechnung beim Einstellungstest aus?
A: Chefs und Verantwortliche für Personal stellen gerne ein paar Aufgaben aus diesen Bereich beim Einstellungstest. Wie bereitet man sich darauf vor? Teilweise werden die Fragen im Gespräch gestellt. Daher hilft es die Formeln auswendig zu wissen und auch zu wissen, wofür die Variablen dafür stehen. Ein kleines bisschen Kopfrechnen schadet auch nicht. Daher die Empfehlung: Lest die oben verlinkten Artikel durch und macht zu den Inhalten die Übungen.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
