Satz des Pythagoras Herleitung und Beweis
Geschrieben von: Dennis RudolphSonntag, 02. Dezember 2018 um 15:22 Uhr
Die Herleitung bzw. den Beweis für den Satz des Pythagoras findet ihr hier. Folgende Inhalte werden angeboten:
- Eine Erklärung, wie man den Satz des Pythagoras herleitet.
- Beispiele wie man den Satz des Pythagoras beweist.
- Übungen damit ihr die Gleichung praktisch üben könnt
- Videos zur Herleitung von a2 + b2 = c2.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Wir sehen uns hier die Herleitung vom Satz des Pythagoras an. Falls ihr euch nur für die Anwendung interessiert seht bitte in Satz des Pythagoras rein. Hilfreich ist auch wenn ihr die Fläche von einem Dreieck berechnen könnt.
Herleitung / Beweis Pythagoras Grundlagen
Es gibt hunderte von Möglichkeiten den Satz des Pythagoras zu beweisen. So viele Herleitungen möchten wir hier natürlich nicht machen. In diesem Abschnitt sehen wir uns jedoch einen Beweis an, der stark grafisch / geometrisch ist und daher hoffentlich einfach verstanden werden kann.
Dazu nehmen wir uns ein Dreieck mit einem rechten Winkel. Dieses hat die Katheten a und b und die längste Seite ist die Hypotenuse c.
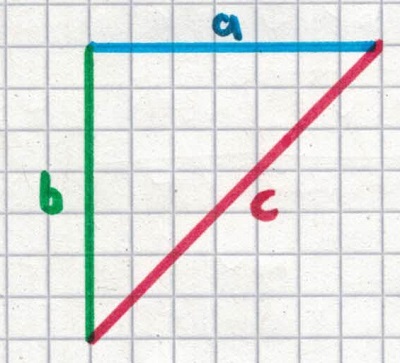
Aus der roten Hypotenuse c machen wir ein Quadrat.
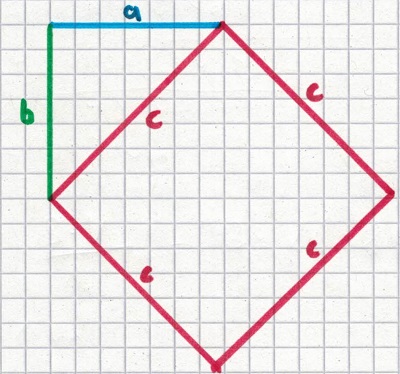
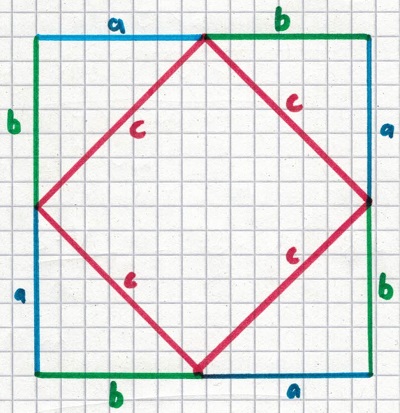
In jeder Ecke vervollständigen wir das Dreieck erneut. Folgendes entsteht:
- Innen entsteht ein rotes Quadrat mit der Seitenlänge c.
- Darum entstehen vier Dreiecke mit je a, b und c als Seiten.
- Außerdem entsteht insgesamt ein Quadrat außen mit a und b auf jeder Seite.
Anzeige:
Anzeigen:
Herleitung / Beweis Pythagoras Formel
Mit diesem Wissen aus dem letzten Abschnitt können wir anfangen zu rechnen. Beginnen wir dabei zunächst mit dem äußeren Quadrat:
- Jede der vier Seiten besteht dabei aus a und b.
- Jede Seite hat damit die Länge a + b.
- Die Länge von dem Quadrat ist damit a + b.
- Die Breite von dem Quadrat ist damit a + b.
- Die Fläche von einem Rechteck ist Länge mal Breite.
- Wir erhalten damit (a + b)·(a + b) für das äußere Quadrat.
Die Fläche wird mit A bezeichnet. Das Quadrat außen hat zusammengefasst A = (a + b)(a + b) = (a + b)2.
Fläche äußeres Quadrat:
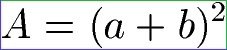
Wie kann man diese Fläche noch berechnen? Man könnte doch auch dies tun:
- Die Fläche vom inneren (roten) Quadrat nehmen.
- Die Fläche der vier Dreiecke außenherum berechnen.
- Diese beiden Flächen rechnen wir zusammen und erhalten ebenfalls das äußere Quadrat.
Fläche inneres Quadrat (rotes Quadrat):

Fehlen uns noch die Dreiecke außen. Eines der Dreieck hat die Fläche 0,5 · a · b. Wir haben vier Dreiecke, also das Ganze mal 4.
Fläche vier Dreiecke:
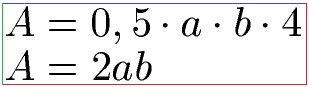
Die Fläche von unserem äußeren Quadrat mit A = (a + b)2 muss so groß sei wie die Fläche vom inneren (roten) Quadrat mit A = c2 plus der Fläche der vier Dreiecke mit A = 2ab:
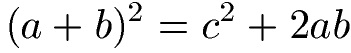
Wie multiplizieren die linke Seite aus und entfernen auf beiden Seiten der Gleichung 2ab. Damit erhalten wir die bekannte Formel a2 + b2 = c2.
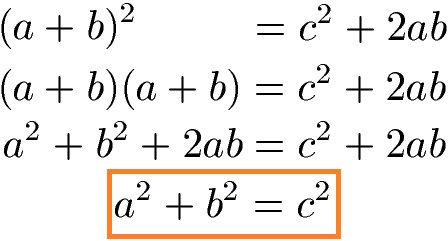
Video Herleitung Satz des Pythagoras
Satz des Pythagoras Herleitung bzw. Beweis
In diesem Video seht ihr eine Herleitung bzw. ein Beweis für den Satz des Pythagoras. Dies wird geometrisch durch den Einsatz von Flächen (und des Geodreiecks) gezeigt und es werden die nötigen Gleichungen aufgestellt. Alles wird Schritt für Schritt an der Tafel gezeigt. Quelle: Youtube.com
Nächstes Video »
Fragen mit Antworten Pythagoras Herleitung / Beweis
In diesem Abschnitt sehen wir uns typische Fragen mit Antworten zur Herleitung bzw. Beweis zum Satz des Pythagoras an.
F: Welche typischen Fehler werden beim Satz des Pythagoras oft gemacht?
A: Diese Schwierigkeiten sieht man oft:
- Das Quadrieren oder Wurzel ziehen nur mit den Zahlen durchführen, aber nicht mit den Einheiten (wird oft falsch gemacht)
- Quadriert ihr Meter (m) erhaltet ihr Quadratmeter (m2).
- Und umgekehrt: Wird beim Wurzelziehen aus m2 wieder m.
- Außerdem müsst ihr darauf achten gleiche Einheiten zu verwenden.
- Ihr dürft nicht Meter und Zentimeter vermischen. Oder andere Einheiten vermischen.
F: Welche Gebiete sollte ich mir als nächstes ansehen?
A: Werft noch einen Blick auf diese Themen:
- x-y-Koordinatensystem
- Begriffe Geometrie
- Quadrat
- Rechteck
- Dreieck
- Viereck
- Quader
- Figur drehen, verschieben und spiegeln
- Kreiszahl Pi
- Prisma Formeln: Volumen und Oberfläche
- Dreieck konstruieren (zeichnen)
- Kongruenzsatz SSS, SWS, WSW und SSW
- Satz des Thales
- Parallelogramm: Eigenschaften und Formeln
- Trapez: Eigenschaften und Formeln
- Strahlensatz
- Zentrische Streckung
- Fläche (Flächeninhalt) berechnen mit Formel
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
