Satz des Pythagoras / Winkel berechnen

An einem rechtwinkligen Dreieck kann man nicht nur den Satz des Pythagoras anwenden, sondern auch die Größe der Winkeln berechnen. Dazu muss man erkennen was Ankathete, Gegenkathete und Hypotenuse sind. Folgende Inhalte werden angeboten:

• Eine Erklärung, wie man den Satz des Pythagoras und die Winkelfunktionen einsetzt.
• Beispiele zum Verwenden von Sinus, Kosinus und Tangens.
• Übungen damit ihr dies alles selbst üben könnt.
• Ein Video zur Nutzung der Winkelfunktionen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wenn ihr Probleme bekommt mit dem Verständnis der nächsten Inhalte, dann werft einen Blick auf diese Inhalte: Dreieck und Wurzel ziehen sowie Wurzelgesetze.

Winkel berechnen und Pythagoras

Zunächst nehmen wir ein Dreieck mit einem rechten Winkel. Außerdem wurde links unten der Winkel Alpha eingetragen. Werft zunächst einen Blick auf das Dreieck, im Anschluss werden dazu ein paar Dinge erklärt.

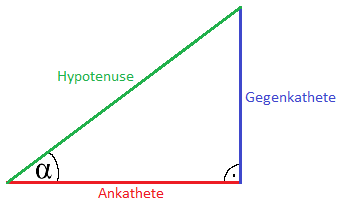
In der Grafik wurden Ankathete, Gegenkathete und Hypotenuse eingetragen. Dies sind wichtige Begriffe, die wir im Anschluss noch brauchen werden.

• Hypotenuse: Die Hypotenuse ist die längste Seite in einem rechtwinkligen Dreieck. Sie liegt gegenüber dem rechten Winkel.
• Gegenkathete: Die Gegenkathete liegt gegenüber dem Winkel Alpha, daher der Name Gegenkathete.
• Ankathete: Die Ankathete liegt am Winkel Alpha.

Merkt euch:

Hat man bestimmt welche Seite was ist, kann man damit auch die Winkel im Dreieck berechnen. Dazu verwendet man die Winkelfunktionen Sinus, Kosinus und Tangens. Die drei Gleichungen sind diese:

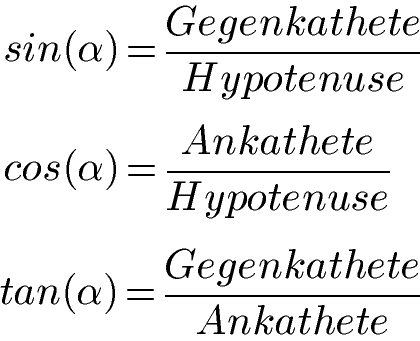
Zur Erinnerung noch die Formel hinter dem Satz des Pythagoras:

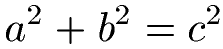
Wer davon noch keine Ahnung hat sieht bitte erst einmal in Satz des Pythagoras rein. Ansonsten findet ihr im nächsten Abschnitt Beispiele zu den Winkelfunktionen.

Anzeige:

Beispiele Winkel berechnen und Pythagoras

In diesem Abschnitt soll gezeigt werden, wie man die Winkel in einem rechtwinkligen Dreieck berechnet sowie die Länge der Seiten.

Beispiel 1: Winkelfunktionen und Pythagoras

Wir haben ein rechtwinkliges Dreieck wie in der nächsten Grafik zu sehen. Berechne die Länge der dritten Seite sowie die Größe der beiden Winkel.

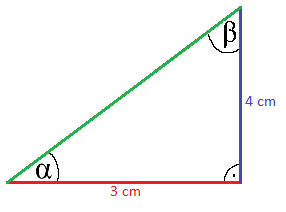
Lösung:

Dritte Seite berechnen:

Es gibt verschiedene Möglichkeiten die Winkel und die Längen zu berechnen. Damit ihr den Umgang damit lernt, gehen wir einige der Wege einmal. Die Hypotenuse können wir mit der Formel hinter dem Satz des Pythagoras lösen. Wir setzen a und b ein und lösen nach c auf.

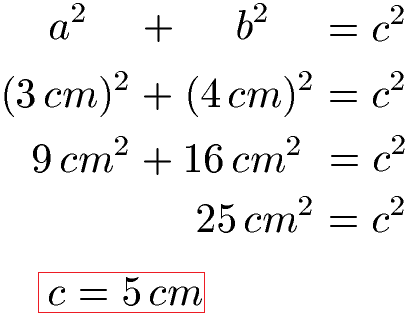
Wir ergänzen die Hypotenuse mit 5 cm in unserer Grafik.

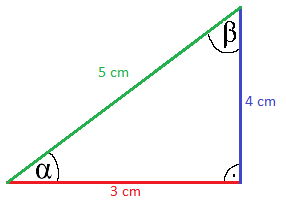
Ankathete, Gegenkathete und Hypotenuse:

Fehlen uns noch die Winkel. Zunächst soll der Winkel Alpha in der linken unteren Ecke berechnet werden. Um dies zu tun, muss zunächst einmal geklärt werden, wo Ankathete, Gegenkathete und Hypotenuse liegen. Bezogen auf den Winkel Alpha gilt:

• Die Hypotenuse ist die längste Seite. Die grüne Seite ist damit die Hypotenuse.
• Die Ankathete ist die Kathete am Winkel, also die rote Seite in unserer Grafik.
• Die Gegenkathete liegt gegenüber dem Winkel, ist damit die blaue Seite.

Mit Sinus berechnen:

Die erste Möglichkeit besteht darin den Winkel Alpha mit dem Sinus zu berechnen. Der Sinus von Alpha ist die Gegenkathete von Alpha geteilt durch die Hypotenuse. Wir setzen diese mit 4 cm und 5 cm ein und berechnen 4 cm : 5 cm = 0,8. Die dritte Zeile ergibt damit, dass der Sinus von Alpha gleich 0,8 ist.

Wir möchten jedoch nicht den Sinus von Alpha, sondern nur Alpha. Daher müssen wir das "sin" noch wegbekommen. Dazu benötigen wir die Umkehrung von "sin" welche man als arcsin oder sin^-1 bezeichnet. Die meisten Taschenrechner haben eine entsprechende Taste. Diese verwenden wir und berechnen den arcsin von 0,8. Der Winkel Alpha ist damit 53,13 Grad groß.

Wichtig: Der Taschenrechner muss für die korrekte Berechnung auf DEG stehen.

Mit Kosinus berechnen:

Anstatt dem Sinus kann auch der Kosinus für die Berechnung des Winkels verwendet werden. Die Seite an Alpha ist die Ankathete, in unserem Fall die rote Seite mit 3 cm. Die Hypotenuse ist die längste Seite in grün mit 5 cm. Der Bruch ergibt 0,6. Der Kosinus von Alpha ist 0,6. Wir suchen jedoch nicht den Kosinus von Alpha sondern nur Alpha.

Dazu benötigen wir die Umkehrung von "cos" welche man als arccos oder cos^-1 bezeichnet. Die meisten Taschenrechner haben eine entsprechende Taste. Diese verwenden wir und berechnen den arccos von 0,6. Der Winkel Alpha ist damit 53,13 Grad groß. Bitte wieder darauf achten, dass der Taschenrechner auf DEG stehen muss.

Mit Tangens berechnen:

Neben Sinus und Kosinus kann der Winkel auch mit dem Tangens berechnet werden. Dazu brauchen wir die Gegenkathete und die Ankathete. Gegenüber dem Winkel Alpha ist ist blau die Gegenkathete gezeichnet und 4 cm lang. Die Ankathete liegt am Winkel (daher Ankathete) und ist in rot eingezeichnet bzw. 3 cm lang. Der Bruch ergibt 1,333. Auch hier suchen wir nicht den Tangens von Alpha sondern nur Alpha. Die Umkehrung führen wir wieder mit arctan bzw. tan^-1 durch. Den Taschenrechner auf DEG stellen ergibt erneut 53,13 Grad.

Beta berechnen:

Die Summe aller Innenwinkel in einem Dreieck beträgt 180 Grad. Wir haben einen rechten Winkel mit 90 Grad und Alpha wurde mit 53,13 Grad berechnet. Der Rest entfällt auf Beta:

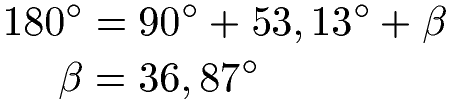
Der Winkel Beta ist etwa 36,87 Grad groß.

Dritte Seite anders berechnen:

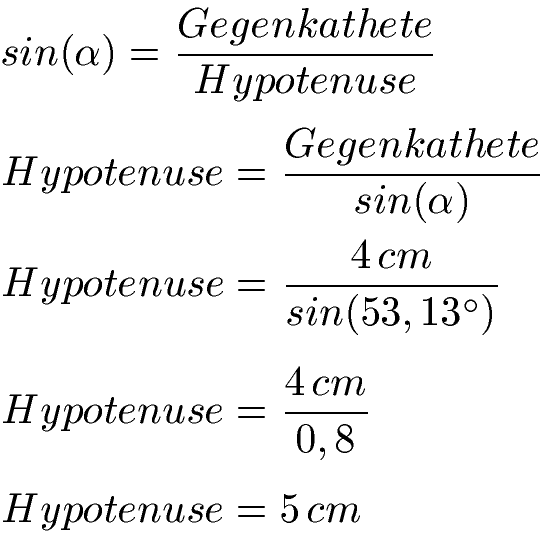
Es gibt noch weitere Möglichkeiten die Hypotenuse zu berechnen. Kennen wir Beispielsweise Alpha mit 53,13 Grad und die Gegenkathete zu Alpha in blau mit 4 cm können wir mit dem Sinus die Hypotenuse berechnen. Daher noch einmal die Grafik:

Der Sinus von Alpha ist dabei - wie immer - die Gegenkathete geteilt durch die Hypotenuse. Die Gleichung stellen wir um nach der Hypotenuse. Danach setzen wir die 4 cm für die Gegenkathete ein und für Alpha 53,13 Grad. Wir berechnen den Sinus mit dem Taschenrechner (auf DEG) stellen. Damit erhalten wir die Hypotenuse mit einer Länge von 5 cm.

Aufgaben / Übungen Winkelfunktionen

Aufgabe 1: Viele Schüler und Schülerinnen scheitern nicht am Rechnen mit ein paar Zahlen sondern finden nicht die richtigen Angaben für die Formeln. Daher starten wir hier erst einmal mit ein paar einfachen Fragen (wer dies nicht mag kann auf überspringen klicken). Zur ersten Frage: Die grüne Seite nennt man ....

• Hypotenuse
• Kathete
• Gegenkathete
• Ankathete

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 8 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Winkel berechnen

Fragen mit Antworten Pythagoras / Winkel berechnen