Satzgruppe des Pythagoras

Was man unter der Satzgruppe des Pythagoras versteht, lernt ihr hier. Folgende Inhalte werden angeboten:

• Eine Erklärung, was man unter der Satzgruppe des Pythagoras versteht.
• Beispiele und Formeln mit Zahlen und Einheiten werden vorgestellt.
• Übungen damit ihr dies selbst üben könnt.
• Video rund um die Satzgruppe des Pythagoras.
• Ein Frage- und Antwortbereich zu diesem Thema.

Hinweis: Zur Satzgruppe des Pythagoras gehören drei Gebiete. Wer sich diese einzeln ansehen möchte wirft bitte direkt einen Blick in Satz des Pythagoras, Kathetensatz und Höhensatz.

Satzgruppe des Pythagoras

Wie bereits in der Einleitung angedeutet, umfasst die Satzgruppe des Pythagoras diese drei Sätze:

• Satz des Pythagoras
• Kathetensatz des Euklid
• Höhensatz des Euklid

Wir werfen hier einen kurzen Blick auf diese drei Themen.

Satz des Pythagoras:

Der Satz des Pythagoras ist ein ganz typisches Thema aus dem Bereich der Geometrie. Wichtig ist erst einmal zu verstehen, wofür man den Satz des Pythagoras überhaupt braucht:

Die nächste Grafik zeigt ein Dreieck mit rechtem Winkel, an welchem man den Satz des Pythagoras anwenden kann:

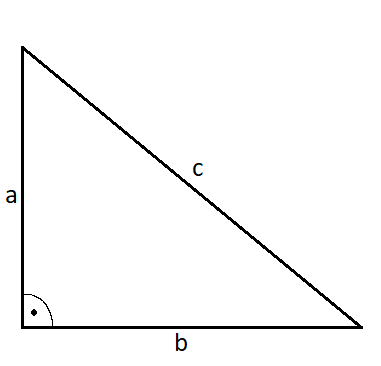
Der 90 Grad Winkel befindet sich in der linken, unteren Ecke. An den rechten Winkel Grenzen die Seiten a und b an, welche man als Katheten bezeichnet. Die längste Seite ist c und wird Hypotenuse genannt. Folgende Gleichung wird im Zusammenhang mit dem Satz des Pythagoras am häufigsten verwendet:

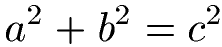
Beispiel 1: Satz des Pythagoras

Wir haben das folgende Dreieck. Berechne die Länge der Hypotenuse c.

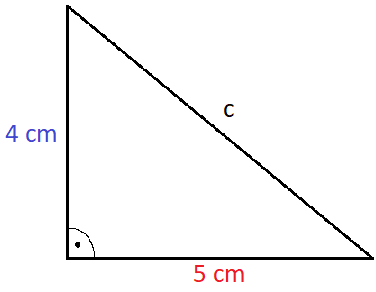
Lösung:

Die Katheten des Dreiecks sind 4 cm und 5 cm lang. Wir stellen die Gleichung vom Satz des Pythagoras nach c um und setzen diese beiden Angaben ein. Wir berechnen die Quadrate und beachten dabei, dass sowohl die Zahlen als auch die Einheiten quadriert werden müssen. Wir fassen zusammen und ziehen die Wurzel. Für die Länge der Hypotenuse "c" erhalten wir etwa 6,4 cm.

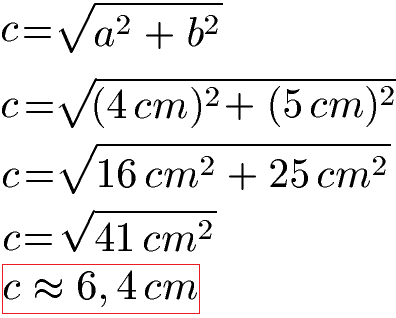
Weitere Erklärungen und Beispiele findet ihr unter Satz des Pythagoras.

Anzeige:

Satzgruppe Pythagoras: Höhensatz und Kathetensatz

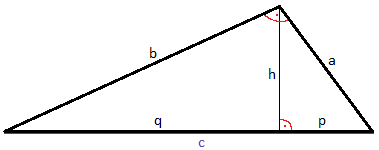
Zur Satzgruppe des Pythagoras gehören auch der Höhensatz und der Kathetensatz. Starten wir mit dem Höhensatz. Auch dieser wird an einem rechtwinkligen Dreieck angewendet, welches jedoch eine Höhe h aufweist.

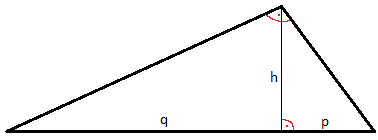
Die Formel zum Höhensatz stellt den Zusammenhang zwischen Höhe und den Achsenabschnitten p und q her.

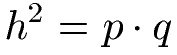
Diese Formel kann man natürlich direkt nach h umstellen oder auch nach p oder q.

Beispiel 2: Höhensatz

Wir haben ein Dach wie in der nächsten Grafik zu sehen. Von der Spitze mit einem rechten Winkel geht eine Höhe h nach unten auf den Dachboden. Bekannt sind außerdem auf dem Boden die beiden Längen 6 Meter und 4 Meter. Wie groß ist die Höhe h?

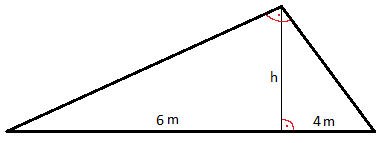
Lösung:

Die beiden Angaben zeigen im Vergleich zur normalen Grafik, dass q = 6 m ist und p = 4 m. Wir suchen die Höhe h, daher nehmen wir die Formel vom Höhensatz nach h umgestellt. In diese Formel setzen wir die Angaben ein und berechnen die Höhe h.

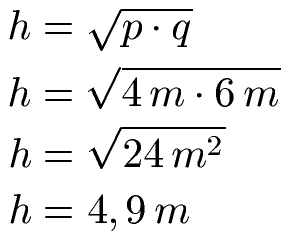
Weitere Erklärungen und Beispiele findet ihr unter Höhensatz des Euklid.

Kathetensatz:

Der Kathetensatz des Euklid gehört auch zur Satzgruppe des Pythagoras. Beim Kathetensatz werden p und q als Hypotenusenabschnitte bezeichnet. Es gilt: Das Quadrat der Länge einer Kathete ist von der Fläche genau so groß wie das Rechteck aus dem zugehörigen Hypotenusenabschnitt und der gesamten Hypotenuse.

Die Gleichungen lauten

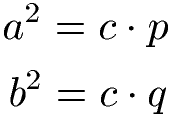
Weitere Erklärungen und Beispiele findet ihr unter Kathetensatz.

Aufgaben / Übungen Satzgruppe Pythagoras

Wir haben sowohl zum Satz des Pythagoras als auch zum Höhensatz und zum Kathetensatz einige Übungen verfügbar. Die Liste wird ergänzt mit einigen Übungen zu den Winkelfunktionen Sinus, Kosinus und Tangens.

• Satz des Pythagoras Aufgaben / Übungen
• Winkelfunktionen Aufgaben / Übungen
• Kathetensatz Aufgaben / Übungen
• Höhensatz Aufgaben / Übungen

Tipp:

• Alle Übungen durchmachen.
• So werdet ihr fit in Mathematik.
• Schummelt nicht beim Lösen der Übungen.

Anzeigen:

Video Satz des Pythagoras

Fragen mit Antworten Satzgruppe Pythagoras