Linearfaktorzerlegung, Linearfaktor und Linearfaktorform

Was man unter einer Linearfaktorzerlegung versteht, lernt ihr hier. Folgende Inhalte werden angeboten:

• Eine Erklärung, was was man unter der Linearfaktorzerlegung versteht.
• Beispiele um eine Zerlegung in Linearfaktoren zu zeigen.
• Übungen zur Linearfaktorzerlegung.
• Ein Video zu diesem Gebiet.
• Ein Frage- und Antwortbereich zu diesem Thema.

Hinweis: Wir sehen uns hier gleich die Linearfaktorzerlegung an. Es sollte euch helfen, wenn ihr bereits wisst, wie die PQ-Formel funktioniert sowie die Polynomdivision. Noch keine Ahnung davon? Werft erst einen Blick in die beiden genannten Themen zum Lösen von quadratischen Gleichungen und macht dann hier weiter.

Linearfaktorzerlegung Erklärung

Wozu braucht man die Linearfaktorzerlegung?

In den meisten Fällen liegt eine Funktion in dieser Schreibweise vor.

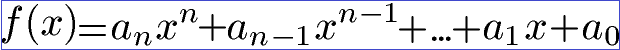
Für die Linearfaktorzerlegung muss die Funktion in diese Schreibweise gebracht werden:

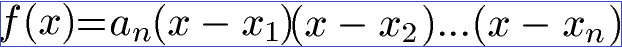
Das x - x₁ oder auch x -x₂ bezeichnet man als einzelne Linearfaktoren.

Beispiel für Linearfaktorzerlegung:

Dies habt ihr noch nicht verstanden? Sehen wir uns ein Beispiel für die Zerlegung in Linearfaktoren an.

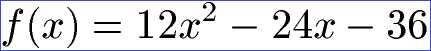
In der Linearfaktordarstellung wäre diese Gleichung wie folgt zu schreiben:

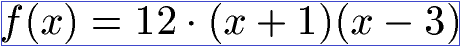
Wie kommt man von der Polynomschreibweise zur Linearfaktorzerlegung?

Anzeige:

Beispiel Linearfaktorzerlegung

Sehen wir uns noch Beispiele für die Linearfaktorzerlegung für eine quadratische Funktion (Gleichung), eine kubische Funktion 3. Grades (ganzrationale Funktion) und eine gebrochenrationale Funktion an.

Beispiel 1: Linearfaktorform quadratische Funktion

Geben Sie die Linearfaktorzerlegung für die folgende Gleichung an.

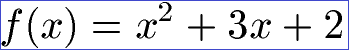
Lösung:

Wir setzen diese Gleichung gleich Null. Mit der PQ-Formel lösen wir die quadratische Gleichung um x₁ und x₂ zu berechnen.

Als Lösung erhalten wir x₁ = -1 und x₂ = -2. Damit eine der Klammern Null wird muss entweder -1 oder -2 für x eingesetzt werden. Daher erhalten wir als Linearfaktorzerlegung (x + 1)(x + 2).

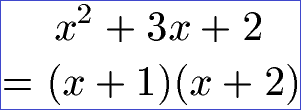
Beispiel 2: Ganzrationale Funktion (Kubische Funktion)

Im zweiten Beispiel soll die Linearfaktorform für eine ganzrationale Funktion gefunden werden. Es handelt sich dabei um eine Gleichung dritten Grades, sprich eine kubische Gleichung. Forme so um, dass die Gleichung in Linearfaktoren zerlegt wird. Um auf die Linearfaktorform zu kommen muss zunächst eine Polynomdivision gerechnet werden.

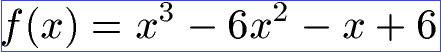
Lösung:

Dazu fehlt uns zunächst eine erste Nullstelle für die Berechnung. Diese finden wir durch Raten von x = 1. Wie dies geht lernt ihr im Artikel Erste Nullstelle finden (Polynomdivision). Wer mit der folgenden Berechnung zu kämpfen hat sieht bitte rein unter Polynomdivision Erklärung.

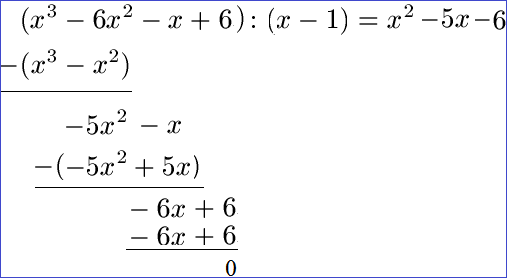
Mit (x -1) kennen wir bereits den ersten Linearfaktor vom Raten der ersten Nullstelle. Übrig geblieben ist noch x² -5x -6. Wir wenden darauf die PQ-Formel an und erhalten x = +6 und x = -1. Die Linearfaktorform sieht dadurch wie folgt aus:

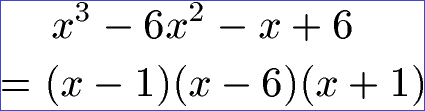
Beispiel 3: Gebrochenrationale Gleichung

Im dritten Beispiel liegt eine gebrochenrationale Gleichung vor. Der Zähler entspricht der Polynomfunktion aus Beispiel 1. Im Nenner liegt die quadratische Gleichung aus Beispiel 2 vor.

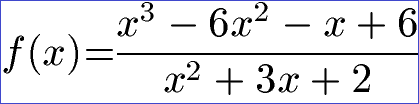
Lösung:

Für Zähler und Nenner soll soll eine Linearfaktorzerlegung durchgeführt werden. Im Zähler des Bruchs machen wir dies wie in Beispiel 1 dargestellt mit Polynomdivision und PQ-Formel und erhalten (x -1)(x - 6)(x + 1). Im Nenner des Bruchs wenden wir die PQ-Formel an wie in Beispiel 2 und erhalten (x + 1)(x + 2). Als Letztes kürzen wir (x + 1) in Zähler und Nenner des Bruchs.

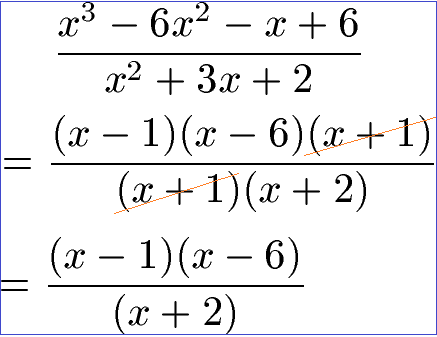
Aufgaben / Übungen Linearfaktorzerlegung

Aufgabe 1:

• Gegeben sei f(x) = x² - 2x - 8.
• Es soll eine Zerlegung in Linearfaktoren durchgeführt werden.
• Wie lautet die Produktdarstellung?

• ( x - 5 ) ( x + 3 )
• ( x + 4 ) ( x - 2 )
• ( x - 4 ) ( x - 2 )
• ( x - 4 ) ( x + 2 )

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Linearfaktorform

Fragen mit Antworten zur Linearfaktorzerlegung