Vektorrechnung Aufgaben / Übungen

Aufgaben bzw. Übungen zur Vektorrechnung und deren Anwendung für die Oberstufe und Abitur findet ihr hier. Wir sehen Vektoren, Koordinatensysteme und im Anschluss die Anwendung in Form von Geraden und Ebenen an.

Es folgt erst einmal eine Liste an Aufgaben zur Vektorrechnung, welche bei uns derzeit verfügbar sind. Die Liste wird regelmäßig erweitert, sobald neue Übungsthemen vorliegen. Unterhalb der Liste erhaltet ihr noch einen Auszug aus den Themen.

Vektorrechnung Aufgaben:

• Räumliches Koordinatensystem Aufgaben / Übungen
• x-y-z Koordinatensystem Aufgaben / Übungen
• Punkte in Koordinatensystem Aufgaben / Übungen
• Vektoren Grundlagen Aufgaben / Übungen
• Vektoren Länge Aufgaben / Übungen
• Vektor Addition und Subtraktion Aufgaben / Übungen
• Skalarprodukt Aufgaben / Übungen
• Kreuzprodukt (Vektorprodukt) Aufgaben / Übungen
• Mittelpunkt einer Strecke Aufgaben / Übungen
• Spatprodukt Aufgaben / Übungen
• Lineare Abhängigkeit Aufgaben / Übungen
• Gerade in Parameterform Aufgaben / Übungen
• Punktprobe bei Vektoren Aufgaben / Übungen
• Ebene in Parameterform Aufgaben / Übungen
• Ebenengleichungen umwandeln Aufgaben / Übungen
• Lagebeziehungen 2 Geraden Aufgaben / Übungen

Worum geht es bei diesen Themen der Vektorrechnung? Dazu mehr im nächsten Abschnitt

Vektorrechnung Aufgaben Grundlagen

In Naturwissenschaften wie zum Beispiel Mathematik und Physik möchte man die Lage und Bewegung von Dingen beschreiben können. Wo befindet sich ein Radiergummi auf einem Tisch? Wo befindet sich ein Flugzeug oder ein Helikopter am Himmel? Stoßen zwei Objekte in der Luft zusammen oder doch nicht?

Koordinatensystem (2D und 3D)

Zum Grundwissen der Vektorrechnung gehört das Koordinatensystem in Ebene und Raum. In diesem kann man zum Beispiel die Position von einem Flugzeug beschreiben. In der Schule zeichnet man zum Beispiel einen Punkt für die Lage eines Objektes in ein Koordinatensystem:

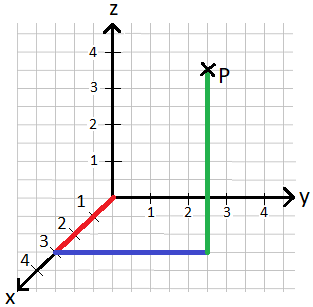
Mehr zum Koordinatensystem unter x-y-z Koordinatensystem und Punkte in Koordinatensystem eintragen.

Anzeige:

Vektoren

Eine Bewegung kann mit Vektoren beschrieben werden: Um von A nach B zu kommen benötigt man diese. Die nächste Grafik zeigt wie so etwas aussehen kann.

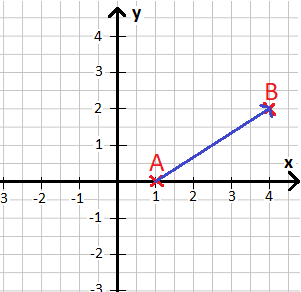
Den Vektor von A nach B schreibt man in der Mathematik so auf:

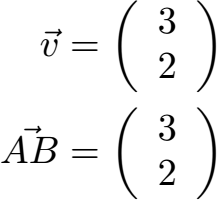
Mehr dazu unter Vektoren Grundlagen.

Vektorrechnung Multiplikation Skalarprodukt

Eine spezielle Art der Multiplikation gibt es in der Vektorrechnung: Das Skalarprodukt ist eine mathematische Verknüpfung von zwei Vektoren bei der eine Zahl als Ergebnis rauskommt. Ein Malzeichen zwischen zwei Vektoren drückt aus, dass das Skalarprodukt berechnet werden soll. Dabei wird das Malzeichen öfters etwas dicker geschrieben Das Skalarprodukt wird zum Beispiel für die Berechnung eines Winkels zwischen zwei Vektoren verwendet.

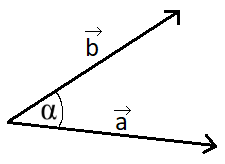
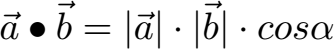
Mehr dazu unter Skalarprodukt berechnen und Skalarprodukt Winkel.

Anzeigen:

Vektorrechnung Erklärung

Wir bieten auch schon eine Reihe an Erklärungen zu den Themen der Vektorrechnung an. Auch diese Liste wird regelmäßig erweitert.

• Räumliches Koordinatensystem
• x-y-z Koordinatensystem
• Punkte in Koordinatensystem
• Vektoren Grundlagen
• Länge (Betrag) eines Vektors
• Vektor Addition und Subtraktion
• Skalarprodukt berechnen
• Skalarprodukt Winkel
• Kreuzprodukt (Vektorprodukt)
• Mittelpunkt einer Strecke
• Spatprodukt
• Lineare Abhängigkeit Vektoren
  • Lineare Abhängigkeit 2 Vektoren
  • Lineare Abhängigkeit 3 Vektoren
• Gerade in Parameterform
• Punktprobe bei Vektoren
• Ebene in Parameterform
• Ebene in Parameterform
• Ebene: Parameterform in Koordinatenform
• Ebene: Parametergleichung in Koordinatengleichung
• Ebene: Parametergleichung in Normalenform
• Ebene: Parametergleichung in Achsenabschnittsform
• Ebene: Koordinatengleichung in Parametergleichung
• Ebene: Koordinatengleichung in Achsenabschnittsform
• Ebene: Koordinatengleichung in Normalenform
• Ebene: Normalenform in Koordinatenform
• Ebene: Normalenform in Parameterform
• Schnittpunkt zweier Geraden
• Schnittwinkel zweier Geraden