Ableitung Wurzel / Wurzelfunktion

Wie man eine Wurzel bzw. Wurzelfunktion ableitet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, wie man eine Wurzelfunktion ableitet.
• Beispiele für die Wurzelableitung mit Potenzregel oder Kettenregel.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur Ableitung einer Wurzel.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Wer mag kann sich die gleich kommenden Ableitungsregeln unter Potenzregel und Kettenregel noch einzeln ansehen.

Ableitung einfache Wurzel

Zunächst ein Hinweis:

Steht nur ein x unter der Wurzel kann die Wurzel in eine Potenz umgewandelt werden. Dies funktioniert auch wenn die 3. Wurzel abgeleitet werden soll. Im Anschluss kann die Funktion mit der Potenzregel abgeleitet werden. Die Formel lautet:

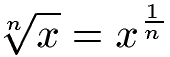
Beispiel 1: Zweite Wurzel Ableitung

Wie lautet die Quadratwurzel aus x abgeleitet?

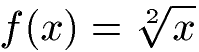
Lösung:

Wir wandeln die Funktion mit der Formel zunächst in eine Potenz um. Im Anschluss nehmen wir die allgemeine Formel für die Ableitung. Diese lautet f'(x) = n · x^n-1. Die Potenz - also 0,5 - kommt damit nach vorne und der Exponent wird um 1 reduziert. Im Anschluss vereinfachen wir die abgeleitete Funktion noch.

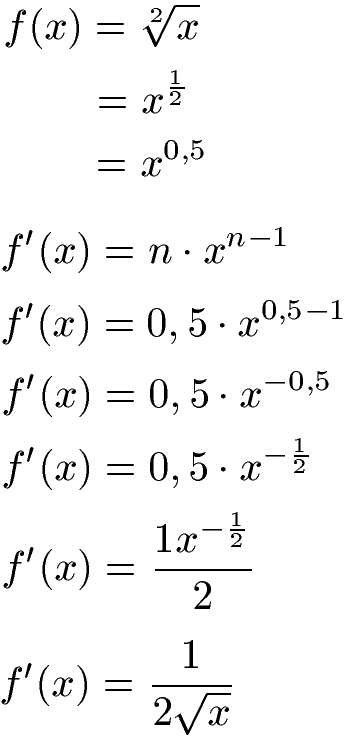
Dies funktioniert natürlich auch wenn wir die n-te Wurzel haben oder dritte Wurzel. In diesem Fall ist n dann eben zum Beispiel 3, aber an der Rechnung ändert sich nichts.

Anzeige:

Ableitung Wurzelfunktion

Was macht man wenn die Funktion mit der Wurzel komplizierter wird? In diesem Fall benötigt man die Kettenregel.

Beispiel 2: Wurzelfunktion ableiten

Wie lautet die erste Ableitung dieser Funktion?

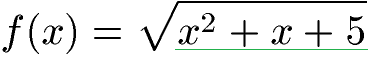
Lösung:

Wir benötigen die Kettenregel für die Ableitung. Dazu unterteilen wir f(x) in eine innere Funktion und eine äußere Funktion. Die innere Funktion ist v(x) = x² + x + 5. Dies abgeleitet ergibt v'(x) = 2x + 1. Als äußere Funktion identifizieren wir die Wurzel von irgend etwas, kurz geschrieben die Wurzel von v. Wirft man einen Blick in eine Ableitungstabelle ist die Wurzel aus v abgeleitet 1 geteilt durch 2 mal Wurzel aus v. Im nächsten Schritt multiplizieren wir innere und äußere Ableitungen miteinander und setzen v = x² + x + 5 wieder ein.

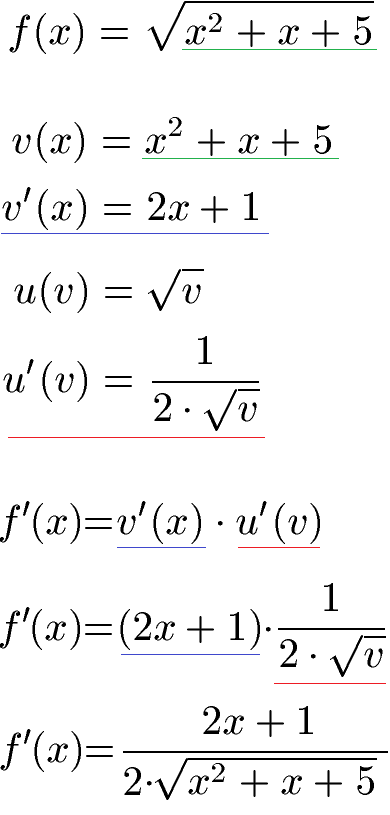
Aufgaben / Übungen Wurzel Ableitung

Aufgabe 1:

Fangen wir mit einer Frage an. Ihr habt eine anspruchsvollere Funktion unter einer Wurzel.

• Welche Ableitungsregel wird für die Wurzelfunktion typischerweise benötigt?

• Kettenregel
• Faktorregel
• Produktregel
• Hypotenusenregel

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Wurzel Ableitung

Fragen mit Antworten Wurzel Ableitung