Ableitung: Grundlagen und Definition (Mathematik)
Geschrieben von: Dennis RudolphSamstag, 09. November 2019 um 17:58 Uhr
Was eine Ableitung in der Mathematik ist und wozu man diese brauch, lernt ihr hier. Dies sehen wir uns an:
- Eine Erklärung, was eine Ableitung ist.
- Beispiele als einfachen Einstieg zu Ableitungen.
- Aufgaben / Übungen um die Grundlagen zur Ableitung zu üben.
- Ein Video zu Ableitungen.
- Ein Frage- und Antwortbereich zu diesem Thema.
Tipp: Wir sehen uns hier die Grundlagen zu Ableitungen an. Viele Vorkenntnisse sind nicht nötig. Hilfreich ist es, wenn ihr jedoch wisst, was eine Funktion ist.
Ableitung Definition und Einleitung
Ableitungen sind ein großes Thema in der 10. Klasse der Schule und in der Oberstufe. Dennoch wissen selbst im Abitur viele Schüler noch nicht wofür man eine Ableitung braucht. Daher sehen wir uns hier erst einmal in einfachen Worten und Grafiken an, wofür man Ableitungen überhaupt braucht und was sie bedeuten.
Für alle, die gerne Abkürzungen nehmen und eine schnelle Definition zur Ableitung brauchen:
Die Ableitung einer Funktion entspricht der Tangentensteigung. Mit der Berechnung von Ableitungen lässt sich das Steigungsverhalten einer Funktion berechnen oder die Steigung der Funktion in einem bestimmten Punkt.
Beispiel Einführung:
Sehen wir uns ein einfaches Beispiel an. Wir haben eine lineare Funktion, welche in rot in das Koordinatensystem eingezeichnet wurde. Wie groß ist dessen Steigung?
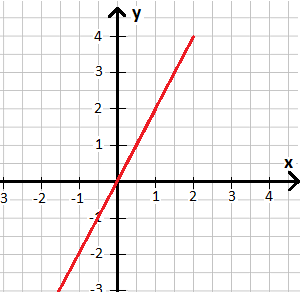
Lösung:
Wir markieren uns zwei Punkte auf dem Verlauf der Funktion und zeichnen ein Steigungsdreieck ein. Wir schreiben uns auf wie lange diese Abschnitte sind.
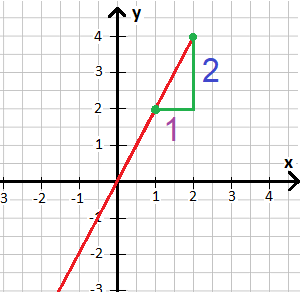
Im Anschluss teilen die Höhe durch die Breite. Dies ist die Steigung, abgekürzt mit "m".
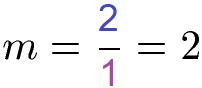
Die Steigung der Funktion ist damit m = 2. In der Mathematik verwendet man dazu auch eine Formel bei der man die Lage der beiden ausgewählten Punkte einsetzt. Ein Punkt wird mit x und y angegeben. In der vorigen Grafik liegt ein Punkt bei P1(1;2) und P2(2;4). Die Steigung lässt sich berechnen, in dem man die beiden y-Werte voneinander subtrahiert und dividiert durch die Subtraktion der beiden x-Werte.
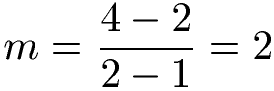
Anzeige:
Anzeigen:
Ableitung Verständnis Beispiel
Das Beispiel aus dem letzten Abschnitt war relativ einfach. Bereits auf den ersten Blick kann man sehen, dass die Steigung überall gleich war. Im nächsten Beispiel haben wir keine lineare Funktion. Dennoch soll die Steigung berechnet werden.
Beispiel 2: Unkonstante Steigung
Die nächste Grafik zeigt eine Funktion, die an unterschiedlichen Stellen verschiedene Steigungen aufweist. Ermittelt werden soll die Steigung im blauen Punkt.
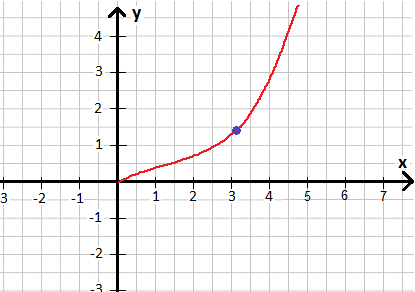
Lösung:
Um die Steigung beim blauen Punkt zu ermitteln, zeichnen wir erneut ein Steigungsdreieck ein. Um das Rechnen zu vereinfachen zeichnen wir das Steigungsdreieck einfach einmal in den Ursprung des Koordinatensystems mit rein (Punkt 0;0).
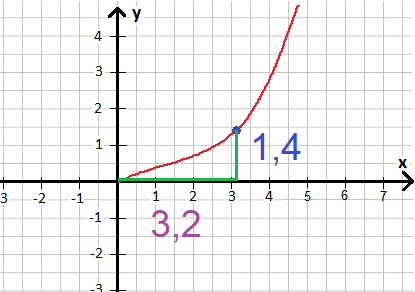
Die Steigung wäre damit:
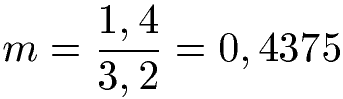
Aber stimmt das eigentlich was wir hier gemacht haben? Wir haben jetzt das Steigungsdreieck einfach über einen bestimmten Bereich gemacht (und zwar vom Ursprung bis zum blauen Punkt). Wir haben also für genau diesen Bereich die Steigung ermittelt. Das war einfach, aber eigentlich nicht genau an diesem Punkt sondern weiter vorne. In der Aufgabenstellung hier es jedoch, dass die Steigung im Punkt gesucht ist. Dies haben wir wenn überhaupt nur sehr grob hinbekommen.
Um die richtige Steigung zu bekommen, müssten wir ein kleines Steigungsdreieck genau dort einzeichnen, wo der Punkt ist um eben genau dort auch die Steigung zu bekommen. Versuchen wir es mal.
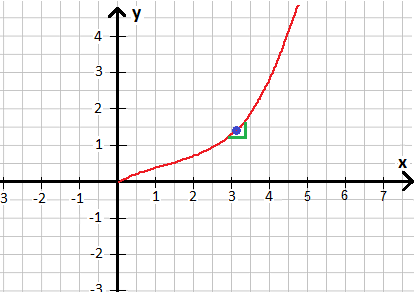
Könnt ihr das noch vernünftig in x und y ablesen um die Steigung zu berechnen? Wird schwierig... Und wenn ihr die Steigung an einer anderen Stelle haben möchtet müsst ihr dort wieder ein Steigungsdreieck einzeichnen und habt erneut das Problem. Hinzu kommt: Das Ablesen geht nur bedingt genau. Ihr macht damit immer Ablesefehler. Es gibt eine bessere Lösung für die Steigung: Die Ableitung mathematisch berechnen.
Die rechnerische Ableitung dient dazu mit Rechenregeln das Steigungsverhalten einer ganzen Funktion zu bestimmen oder per Rechnung die Steigung in einem bestimmten Punkt exakt zu ermitteln.
Soweit eine kurze Einleitung. Um das Rechnen mit Ableitungen zu lernen, sollte man sich mit diesen Themen befassen:
- Den Regeln zur Ableitung von Funktionen / Gleichungen und
- damit die Ableitung verschiedenster Arten von Funktionen
- Was Hochpunkt, Tiefpunkt, Wendepunkt etc. sind und
- welche Bedeutung die verschiedenen Ableitungen haben.
Eines solltet ihr schon Wissen: Die erste Ableitung wird mit f'(x) bzw y' bezeichnet, die zweite Ableitung f''(x) oder y'' und so weiter.
Aufgaben / Übungen zum Ableiten
Anzeigen:Video Ableitung
Näherung und Tangente
Was ist eigentlich eine Ableitung? Und was ist an dieser Stelle? So soll die Frage beantwortet werden: Wie groß ist die Steigung um f(x) an der Stelle x = 0? Die Lösung der Aufgabe wird dabei zunächst mit einer Näherung bestimmt. Im Anschluss wird mit einer Tangenten gearbeitet, ermittelt durch Aufstieg durch Fortschritt. Wir merken: Die Ableitung der Funktion f(x) an der Stelle 0 ist die Steigerung der Tangente f'(x). Dieses Video habe ich auf Youtube.com gefunden.
Nächstes Video »
Fragen mit Antworten Ableiten
In diesem Abschnitt sehen wir uns Fragen mit Antworten zur Ableitung an.
F: Welche Themen sollte ich zur Ableitung lernen?
A: Die folgenden Themen werden in der Schule zu Ableitungen behandelt.
- Differentialrechnung Übersicht
- Ableitung: Grundlagen und Definition
- Ableitung Tabelle / Ableitungstabelle
- Ableitungsregeln
- Kurvendiskussion
F: Wann wird dieses Thema in der Schule / Studium behandelt?
A: Das Ableiten von Funktionen wird meistens ab der 10. Klasse in der Schule behandelt. Ableitungen stehen auch in der Oberstufe und im Abitur auf dem Plan. Ebenfalls werden Ableitungen in vielen Studiengängen behandelt: Darunter in den Naturwissenschaften, in technischen Fächern und auch in vielen Wirtschaftsfächern.
F: Was lernt man nach der Ableitung?
A: Nach den Ableitungen ist das nächste große Themengebiet in der Regel die Integralrechnung. Im Prinzip macht man hier das Umgekehrte der Ableitung.
Neue Artikel
- Raute ▷ Formeln, Eigenschaften und Beispiele
- Sachaufgaben Klasse 5 Mathematik Aufgaben
- Sachaufgaben Mathe: Klasse 5
- Worte in Zahlen Aufgaben (Übungen)
- Worte in Zahlen umwandeln
- Teilerfremdheit (Mathematik)
- Hohlmaße umrechnen
- Hundertertafel Grundschule
- Quersumme berechnen und Teilbarkeit
- Quadratzahlen berechnen (mit Liste)
