Extremwertberechnung

Was die Extremwertberechnung ist und wie man sie durchführt, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was Extremwerte sind und wie man sie berechnet.
• Beispiele wie man die Extremwertberechnung durchführt.
• Aufgaben / Übungen um dies alles selbst zu üben.
• Ein Video zur Berechnung der Extremwerte.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Für die Extremwertberechnung werden verschiedenen Ableitungsregeln benötigt. Insbesondere die Potenzregel solltet ihr kennen. Hilfreich sind jedoch auch weitere Ableitungsregeln.

Extremwertberechnung Erklärung

Klären wir zunächst einmal, was man unter der Berechnung der Extremwerte versteht. Die nächste Grafik zeigt den Verlauf einer Funktion mit Hochpunkten (Max) und Tiefpunkten (Min). Beides sind Extremwerte.

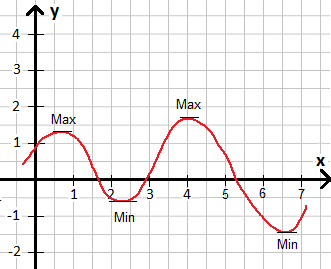
Einen Punkt in der Ebene gibt man mit einem x-Wert und einem y-Wert an. Dies ist auch bei der Extremwertberechnung der Fall, wobei man hier ein bisschen mit den Begriffen aufpassen sollte.

• Der Extrempunkt ist ein Punkt der mit x und y angegeben wird
• Die Extremstelle ist nur der x-Wert davon.
• Der Extremwert ist nur der y-Wert davon.

In der Praxis ist es so, dass man die volle Berechnung vom Extrempunkt durchführen muss und man sich für die Extremwertberechnung davon einfach nur den y-Wert nimmt.

Die Extremwertberechnung wird aus diesem Grund wie folgt durchgeführt:

• 1. Ableitung Null setzen, f'(x) = 0.
  • Dies liefert mögliche Minima und Maxima (x_e genannt).
• Die 2. Ableitung an dieser Stelle x_e muss ungleich 0 sein.
  • Ist f''(x_e) < 0 liegt ein Maxima vor.
  • Ist f''(x_e) > 0 liegt ein Minima vor.
  • Ist f''(x_e) = 0 steht eine Prüfung auf Wendepunkte an.
• Die x_e-Werte werden in die Ausgangsgleichung f(x) eingesetzt um y zu berechnen (Extremwert).

Anzeige:

Berechnung der Extremwerte

Sehen wir uns einmal an, wie man die Extremwertberechnung praktisch durchführt.

Beispiel 1: Extremwert berechnen

Wo liegt der Extremwert der nächsten Funktion?

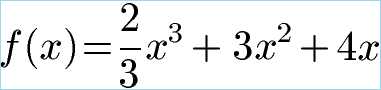
Lösung:

Wir benötigen die Potenzregel um die erste Ableitung zu berechnen.

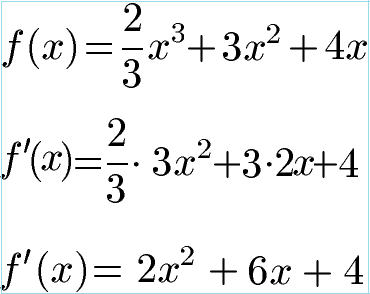
Im zweiten Schritt setzen wir die erste Ableitung gleich Null, also f'(x) = 0. Dies lösen wir mit der PQ-Formel. Dazu lesen wir p = 3 und q = 2 ab und setzen dies in die allgemeine Lösungsgleichung der PQ-Formel ein. Im Anschluss berechnen wir x₁ = -1 und x₂ = -2.

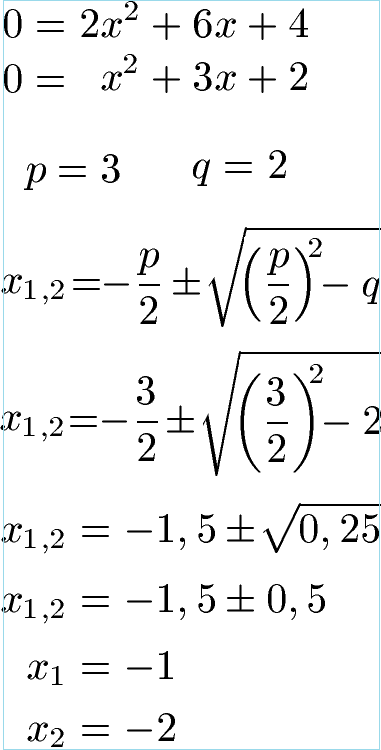
Wir halten fest: Bei x₁ = -1 und x₂ = -2 liegen mögliche Extremwerte, welche wir nun näher untersuchen möchten. Mit der Potenzregel bilden wir noch die 2. Ableitung.

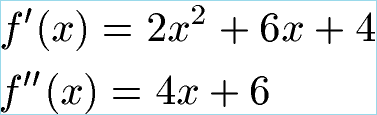
Um zu überprüfen, ob es sich bei x₁ = -1 und x₂ = -2 um einen Extremwert handelt, setzen wir diese beiden x-Werte in f''(x) ein. Ist das Ergebnis größer als Null ist der Punkt ein Minima. Ist das Ergebnis kleiner als Null liegt ein Maxima vor.

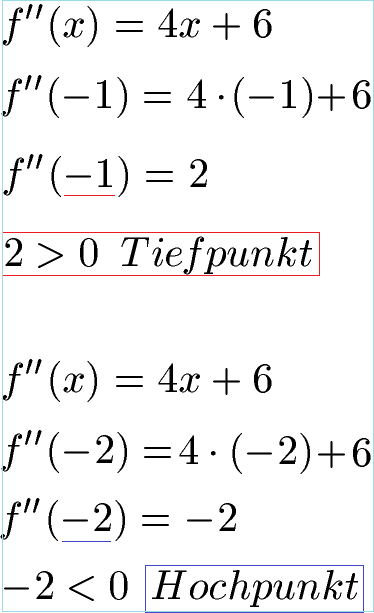
Die Berechnung zeigt, dass bei x₁ = -1 ein Minima vorliegt und bei x₂ = -2 ein Maxima. Wir kennen damit die x-Werte dieser Extrempunkte (also genauer gesagt kennen wir die Extremstelle). Jetzt berechnen wir noch deren y-Werte (also die Extremwerte). Dazu setzen wir x = -1 und x = -2 in die Ausgangsfunktion f(x) ein.

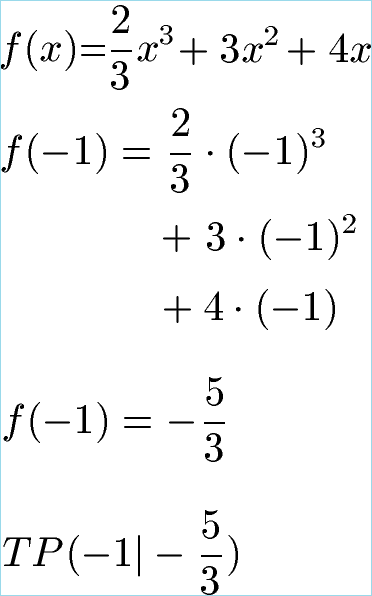
Wo liegen die Extrempunkte? Das Minima liegt bei x = -1 und y = - 5 : 3. Das Maxima berechnen wir gleich noch zu x = -2 und y = - 4 : 3.

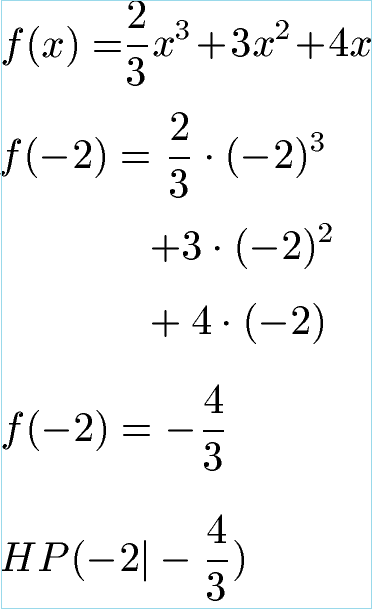
Aufgaben / Übungen Extremwertberechnung

Aufgabe 1:

Wo liegt der Extrempunkt dieser Funktion?

• x = 0, y = -1
• x = 0, y = 0
• x = 1, y = 1
• x = -1, y = 0

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 2 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Extremwertberechnung

Fragen mit Antworten zur Extremwertberechnung