Funktionen ableiten / Gleichungen Ableitung

Was man eine Funktion oder Gleichung ableitet (grafische und rechnerische Ableitung), lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was eine Ableitung ist.
• Beispiele für das Ableiten von Funktionen.
• Aufgaben / Übungen um die Grundlagen zur Ableitung zu üben.
• Ein Video zu Ableitungen.
• Ein Frage- und Antwortbereich zu diesem Thema.

Tipp: Wir sehen uns hier die Grundlagen zur Ableitung von Funktionen bzw. Gleichungen an. Viel müsst ihr dazu erst einmal nicht wissen. Hilfreich ist es jedoch wenn ihr wisst was eine Funktion ist.

Funktion Ableitung Erklärung

Bevor wir uns die Regeln zur Ableitung von Funktionen / Gleichungen ansehen, klären wir erst einmal eine Frage: Was ist eine eine Ableitung?

Sehen wir uns kurz an was dies grafisch bedeutet und im Anschluss sehen wir uns Regeln für die Ableitung von Funktionen an.

Beispiel Ableitung grafisch:

Sehen wir uns eine einfache Aufgabe zur Ableitung an. Wir haben eine lineare Gleichung, welche in rot in das x-y-Koordinatensystem eingezeichnet wurde. Um die Steigung (also die Ableitung) zu berechnen, müssen wir uns zwei Punkte auf dem Verlauf der Funktion einzeichnen sowie ein Steigungsdreieck. Wir schreiben uns auf wie lange diese Abschnitte sind (in y-Richtung 2 und in x-Richtung 1).

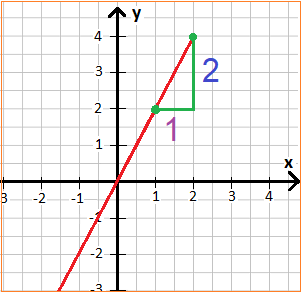
Im Anschluss teilen wir y durch x. Dies ist die Steigung, abgekürzt mit "m".

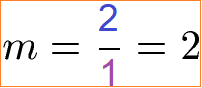
Die Steigung der Funktion ist damit m = 2. In der Analysis verwendet man dazu auch eine Formel bei der man die Lage von zwei ausgewählten Punkten einsetzt. Ein Punkt wird mit x und y angegeben. Bei der eben besprochnen Funktion liegt ein Punkt bei P₁(1;2) und der zweite bei P₂(2;4). Die Steigung der Funktion lässt sich berechnen, in dem man die beiden y-Werte voneinander subtrahiert und dividiert durch die Subtraktion der beiden x-Werte.

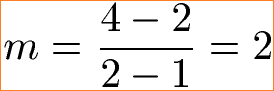
Dies ist natürlich umständlich, denn meistens möchte man eine Funktion nicht zeichnen und außerdem sind Funktionen oft komplizierter, da die Steigung an verschiedenen Stellen unterschiedlich groß ist. Aus diesem Grund gibt es Regeln zur Ableitung von Funktionen. Dazu mehr im nächsten Abschnitt.

Anzeige:

Funktion ableiten Beispiele

Es gibt zahlreiche Ableitungsregeln um Funktionen abzuleiten (Beispiele weiter unten). Für die Ableitung einer einfachen Gleichung reichen Regeln wie die Faktorregel, Potenzregel oder Summenregel. Liegt eine Multiplikation von zwei Funktionen vor, benötigt ihr die Produktregel. Brüche werden mit der Quotientenregel abgeleitet. Sind Funktionen verkettet wie bei Logarithmen, Wurzel, Klammer und E-Funktion wird die Kettenregel benötigt.

• Konstantenregel (Konstante Funktion)
• Faktorregel Ableitung
• Potenzregel Ableitung
• Summenregel / Differenzregel Ableitung
• Produktregel Ableitung
• Quotientenregel Ableitung
  • Bruch Ableitung
• Kettenregel Ableitung
  • Ableitung Logarithmus / Logarithmusfunktion
  • Ableitung ln (natürlicher Logarithmus)
  • Ableitung Wurzel / Wurzelfunktion
  • Ableitung Klammer
  • Ableitung E-Funktion
• Produktregel und Kettenregel gemeinsam

Faktoren ableiten:

Faktoren bleiben bei der Ableitung erhalten:

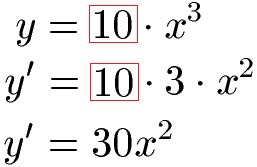
Dieses Beispiel und weitere unter Faktorregel Ableitung.

Potenzen ableiten::

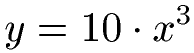
Dieses Beispiel und mehr unter Potenzregel Ableitung.

Summen ableiten:

Summen und Differenzen von Funktionen werden einzeln abgeleitet.

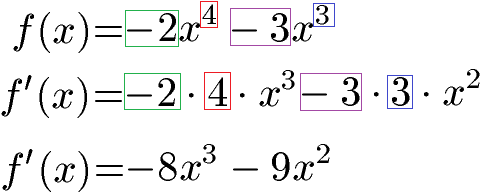
Wie dies geht lernt ihr unter Summenregel / Differenzregel Ableitung.

Produkte Ableitung:

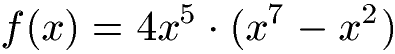
Die Ableitung von Produkten besprechen wir unter der Produktregel Ableitung.

Funktion ableiten Brüche:

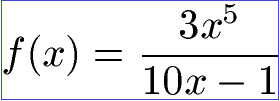
Wie man Brüche ableitet lernt ihr unter Quotientenregel Ableitung oder Bruch Ableitung.

Ableitung Funktion Kettenregel:

Eine Funktion ableiten mit Klammer oder Wurzel könnt ihr mit der Kettenregel. Zum Beispiel solche Funktionen:

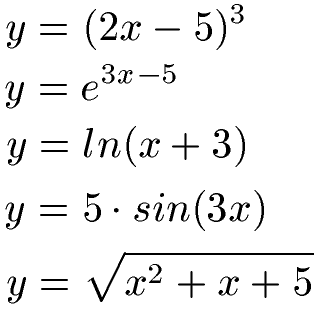
Wie dies geht findet ihr unter Kettenregel Ableitung.

Aufgaben / Übungen Funktion Ableitung

Aufgabe 1:

Bildet man eine Ableitung von einer Funktion / Gleichung, dann interessiert man sich in den meisten Fällen für...

• ... die Fläche
• ... die Steigung
• ... die Wahrscheinlichkeit
• ... den Winkel

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 11 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Ableitung

Fragen mit Antworten zu Funktionen ableiten