Summenregel / Differenzregel Ableitung

Die Summenregel bzw. Differenzregel für Ableitungen lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was die Summenregel / Differenzregel .
• Beispiele wie man diese Ableitungsregel anwendet.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zu Regeln der Ableitung.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es gibt unterschiedliche Regeln um Funktionen oder Gleichungen abzuleiten. Bevor ihr euch diese jedoch anseht, solltet ihr die Grundlagen der Ableitung kennen und die Potenzregel.

Summenregel / Differenzregel Erklärung

Wie kann man Funktionen oder Gleichungen ableiten, wenn diese aus Summen oder Differenzen bestehen? Dazu gibt es die Summenregel oder auch Differenzregel. Sehen wir uns kurz die Formeln zu beidem an und im Anschluss gibt es Beispiele.

Formel Summenregel:

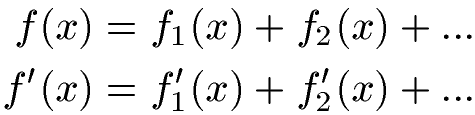
Formel Differenzregel:

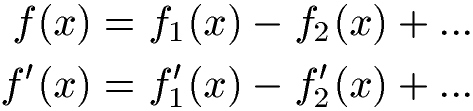
Noch nicht verstanden? Ein paar Beispiele sollten helfen.

Beispiel 1: Summenregel

Sehen wir uns die Ableitungsregel "Summenregel" an. Dabei soll f(x) = 3x + 2 abgeleitet werden. Wir leiten dazu die einzelnen Teile der Funktion ab. Leiten wir 3x ab (mit der Potenzregel) erhalten wir 3. Die Konstante 2 abgeleitet ergibt 0, fällt damit weg.

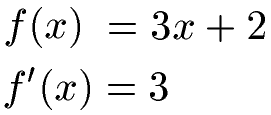
Anzeige:

Summenregel / Differenzregel Beispiele

In diesem Abschnitt sehen wir uns ein weiteres Beispiel zur Differenzregel an und die Summenregel in Verbindung mit der Potenzregel.

Beispiel 2: Differenzregel

Zwischen den Teilen einer Funktion muss nicht ein plus (+) stehen, sondern es kann auch ein (-) stehen. Die Vorgehensweise beim Ableiten ist identisch zur Summenregel von weiter oben. Dabei werden die einzelnen Teile der Funktion erneut separat abgeleitet. Aus 4x wird 4 und aus -2x wird -2.

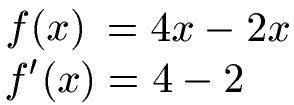
Beispiel 3: Summenregel mit Potenzregel

Im nächsten Beispiel werden sowohl Summenregel als auch Potenzregel benötigt um die Ableitung zu bilden. Dabei bilden wir sowohl von -2x⁴ die Ableitung als auch von -3x³. Bei der Ableitung kommt der Exponent nach vorne in die Basis und der Exponent wird um 1 reduziert.

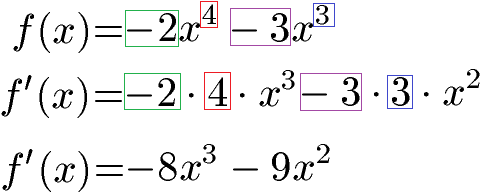
Wichtig: In vielen Fällen müssen mehrere Ableitungsregeln angewendet. Dies funktioniert nur, wenn man diese Regeln der Ableitung kennt.

Aufgaben / Übungen

Aufgabe 1:

Bevor ihr Funktionen ableitet eine kurze Frage davor:

• Was sind Summenregel und Differenzregel?

• Kreisumfang berechnen
• Wurzelfunktionen
• Ableitungsregeln
• Trigonometrische Funktionen

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 4 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Ableitungsregeln

Fragen mit Antworten zu Summen- und Differenzregel