Verhalten im Unendlichen

Was das Verhalten im Unendlichen ist und wie man es berechnet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was man unter dem Verhalten im Unendlichen versteht.
• Beispiele für die Berechnung dieser Grenzwerte.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zu Grenzwerten.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es ist hilfreich, wenn ihr bereits wisst, was ein Bruch ist und wie man eine Funktion zeichnet. Wer davon noch keine Ahnung hat, liest dies bitte erst einmal nach. Ansonsten startet gleich mit dem Verhalten im Unendlichen.

Verhalten im Unendlichen einfach erklärt

Wann und wo sieht man sich das Verhalten im Unendlichen an?

Verhalten im Unendlichen Graph:

Sehen wir uns eine ganz einfache Einleitung zu diesem Thema an. Die nächste Grafik zeigt die Funktion f(x) = x² in ein Koordinatensystem eingezeichnet. Werft einen Blick darauf:

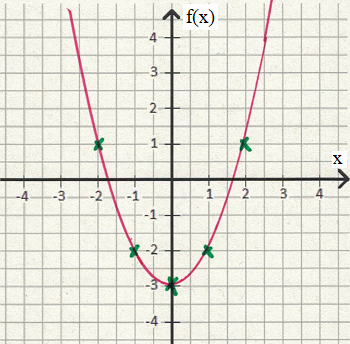
Wie sieht das Verhalten dieser Funktion im Unendlichen aus? Eine Funktion kann man natürlich nicht bis ins Unendliche zeichnen. Aber man sieht hier ganz klar, dass wenn die x-Werte größer werden auch die y-Werte größer werden. Macht man die x-Werte immer kleiner ( -5, -10, -20, -100 und so weiter) werden die y-Werte ebenfalls immer größer.

In beiden Fällen laufen die y-Werte damit gegen unendlich. Das Zeichen für unendlich ist eine "umgefallene" 8. Um zu zeigen, dass man den Grenzwert sucht - also maximal zu einem Ziel strebt - wird der Limes verwendet, abgekürzt lim. Und dann muss man sich entscheiden, ob man gegen plus unendlich laufen möchte (100, 1000, 10000, ...) oder gegen minus unendlich (-100, -1000, -10000, ...).

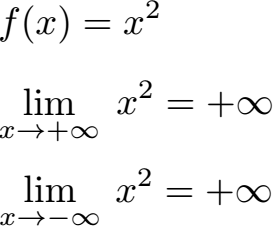
Anzeige:

Verhalten im Unendlichen Beispiele

Bei Funktionen wie y = x² ist es sehr einfach die Grenzwerte - also in unseren Fällen das Verhalten im Unendlichen - zu ermitteln. Wie sieht dies jedoch bei komplizierten Funktionen aus? Dazu sehen wir uns Beispiele für ganzrationale Funktionen, gebrochenrationale Funktionen sowie E-Funktionen an und Wurzeln. Um diesen Artikel nicht extrem in die Länge zu ziehen, zeigen wir euch kurz das Beispiel und verlinken auf die ausführliche und einfach erklärte Lösung darunter.

Die Beispiele findet ihr unter:

• Verhalten im Unendlichen: Ganzrationale Funktionen
• Verhalten im Unendlichen: Gebrochenrationale Funktion
• Verhalten im Unendlichen: E-Funktion / Wurzel

Ganzrationale Funktion

Starten wir mit dem Verhalten im Unendlichen für eine ganzrationale Funktion. Dabei soll das Verhalten gegen plus unendlich und minus unendlich bestimmt werden. Ganzrationale Funktionen sind zum Beispiel:

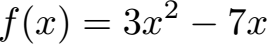
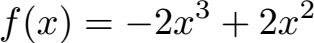
Diese ganzrationalen Funktionen 2. und 3. Grades findet ihr untersucht unter:

• Verhalten im Unendlichen: Ganzrationale Funktionen

Gebrochenrationale Funktion:

Als nächstes sehen wir uns das Verhalten von Funktionen im Unendlichen an wenn diese gebrochenrational sind. Drei Beispiele werden vorgerechnet:

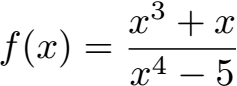
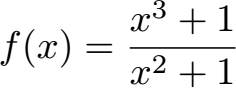
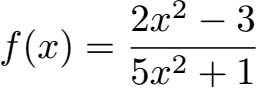
Diese Beispiele rechnen wir vor unter:

• Verhalten im Unendlichen: Gebrochenrationale Funktion

E-Funktion / Wurzel:

Auch bei E-Funktionen und Wurzelfunktionen sieht man sich das Verhalten gegen plus unendlich und minus unendlich an. Diese beiden Beispiele rechnen wir euch vor:

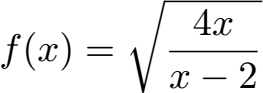
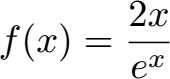
Diese Beispiele rechnen wir vor unter:

• Verhalten im Unendlichen: E-Funktion / Wurzel

Aufgaben / Übungen Verhalten im Unendlichen

Aufgabe 1:

• Wie sieht das Verhalten der folgenden Funktion gegen plus unendlich aus?

• 0
• minus unendlich
• plus unendlich
• kein Grenzwert

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 12 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Grenzwerte

Fragen mit Antworten zum Verhalten im Unendlichen