Konstantenregel / Konstante Funktionen

Die Konstantenregel und konstante Funktionen werden hier behandelt. Dies sehen wir uns an:

• Eine Erklärung, was eine konstante Funktion ist.
• Beispiele für konstante Funktionen und deren Ableitung.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zu Ableitungen.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Um die folgenden Inhalte zu verstehen helfen ein paar Vorkenntnisse wie Grundwissen zu Funktionen und was eine Ableitung ist. Noch keine Ahnung davon? Werft einen Blick auf Funktionen und Ableitung Grundlagen.

Konstante Funktion und Ableitung

Klären wir erst einmal was eine konstante Funktion oder konstante Gleichung ist.

Dies zum Beispiel sind konstante Funktionen:

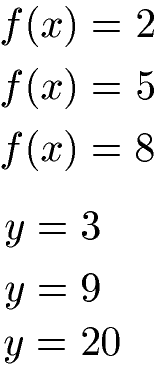
Konstante Funktion Koordinatensystem:

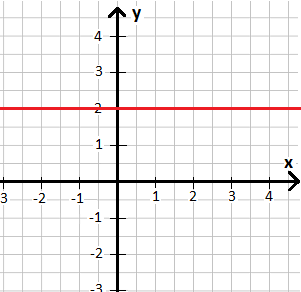
Die folgende Grafik zeigt die Funktion f(x) = 2 in einem Koordinatensystem. Jedem sollte auffallen, dass diese Funktion keine Steigung hat. Dies erkennt man daran, dass der Kurvenverlauf weder ansteigt noch abfällt. Wir halten fest: Die Steigung ist m = 0.

Im nächsten Abschnitt sehen wir uns Ableitung und Steigung noch etwas genauer an.

Anzeige:

Konstantenregel / Ableitungsregel

Für die Ableitung / Steigung einer konstanten Funktion gilt:

Beispiel Ableitung mit Konstantenregel:

Leite die Funktion y = 1 ab. Wie lautet die Ableitung? Wie groß ist die Steigung der Funktion?

Lösung:

Wir bilden die erste Ableitung. Leiten wir einfach die Zahl 1 ab, dann fällt diese weg. Dies bedeutet, dass die erste Ableitung Null ist. Es liegt keine Steigung vor, m = 0.

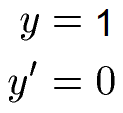
Im Koordinatensystem eingezeichnet ergibt dies:

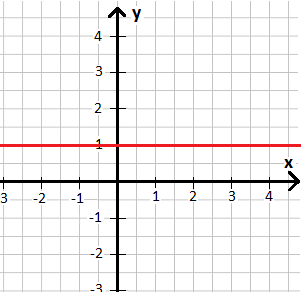
Auch hier kann man sehen, dass es keine Steigung gibt. Denn der Verlauf der Funktion ist weder steigend noch fallend.

Aufgaben / Übungen konstante Funktion

Aufgabe 1:

• Wie sieht die Gleichung einer konstanten Funktion aus?

• y = 3x + 2
• y = -8x
• y = 3x
• y = c

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Ableitungen

Fragen mit Antworten Konstantenregel