Ableitung Logarithmus / Logarithmusfunktion

Wie man einen Logarithmus bzw. eine Logarithmusfunktion ableitet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, wie man Gleichungen mit Logarithmus ableitet.
• Beispiele wie man mit der Kettenregel logarithmen ableitet.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur Ableitungsregeln.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es ist hilfreich wenn ihr bereits wisst was ein Logarithmus ist und die Kettenregel kennt. Wer davon noch keine Ahnung hat wirft einen Blick in die Logarithmus Grundlagen und Kettenregel.

Logarithmus Ableitung Erklärung

Zunächst ein kurzer Hinweis:

Starten wir mit der Ableitung vom natürlichen Logarithmus. Aus einer Tabelle für Ableitungen kann man zunächst die Ableitung von ln(x) entnehmen. Diese ist 1 : x. Dies ist eine wichtige Grundlage für die folgenden Beispiele und Aufgaben.

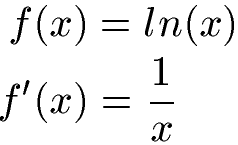
So einfach ist es selten. Daher sehen wir uns anspruchsvollere Logarithmusfunktionen zum Ableiten an.

Beispiel 1: Ableitung Logarithmus

Wie lautet die erste Ableitung der folgenden Logarithmusfunktion?

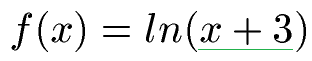
Lösung:

Logarithmusfunktionen werde mit der Kettenregel abgeleitet. Dazu unterteilt man f(x) in eine innere Funktion und eine äußere Funktion und leitet beide jeweils ab. Die innere Funktion ist dabei x + 3, abgeleitet einfach 1. Die äußere Funktion ist der ln von irgendetwas, abgekürzt ln v. Einer Ableitungstabelle kann man entnehmen, dass die Ableitung von ln v einfach 1 : v ist. Beide Ableitungen werden miteinander multipliziert und für v wird v = x + 3 wie am Anfang festgelegt eingesetzt.

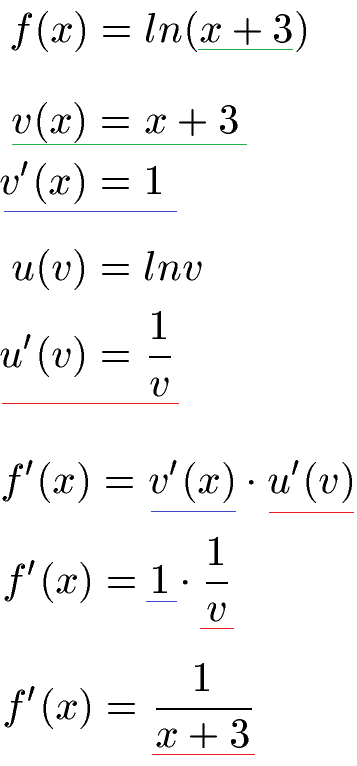
Anzeige:

Logarithmus Ableitung Beispiele

Sehen wir uns ein weiteres Beispiel zum Ableiten von einem natürlichen Logarithmus an.

Beispiel 2: Natürlicher Logarithmus ableiten

Die Ableitung einer Mischung aus natürlichem Logarithmus und Sinus-Funktion soll gefunden werden. Wie lautet die 1. Ableitung dieser Gleichung?

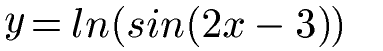
Ein Hinweis: Für die Lösung wird eine Substitution benötigt. Wer nicht mehr weiß was dies ist wirft einen Blick in den Artikel Substitution.

Lösung:

Um Logarithmus-Funktionen abzuleiten, wird die Kettenregel benötigt. Um die Ableitung durchzuführen arbeiten wir uns von innen nach außen. Daher substituieren wir zunächst mit u = 2x - 3. Wir ersetzen also 2x - 3 durch u. Dadurch vereinfacht sich unsere Gleichung zu y = ln (sin(u)). Dies findet man jedoch auch nicht in einer Ableitungstabelle. Daher substituieren wir erneut. Wir ersetzen sin(u) durch v. Unsere Gleichung vereinfacht sich zu y = ln (v).

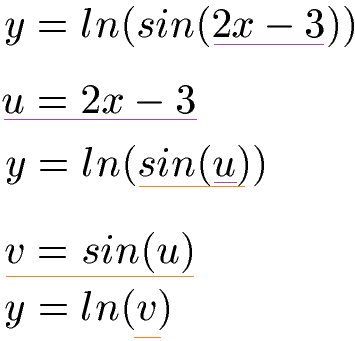
Wir haben nun drei Funktionen gebastelt, die wir jeweils in einer Ableitungstabelle finden können. Diese müssen nach der jeweiligen Variable abgeleitet werden. Aus ln v wird dadurch 1 : v. Aus sin(u) wird cos(u) und 2x - 3 ist abgeleitet 2.

Zuletzt multiplizieren wir die drei Ableitungen miteinander. Dabei sollten wir die Substitutionen rückgängig machen. Wir setzen für u und v wieder alles von oben ein.

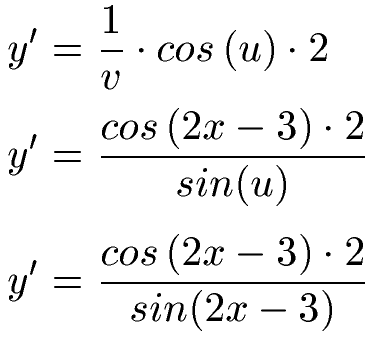
Aufgaben / Übungen Logarithmusableitung

Aufgabe 1:

Bevor wir rechnen erst einmal eine Frage:

• Welche Ableitungsregel wird typischerweise verwendet um Logarithmusfunktionen abzuleiten?

• Produktregel
• Bruchregel
• Quotientenregel
• Kettenregel

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Ableitung Logarithmus

Fragen mit Antworten Logarithmus ableiten