Ableitung E-Funktion

Wie man eine E-Funktion ableitet, lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, warum die E-Funktion so besonders ist.
• Beispiele für das Ableiten von E-Funktionen.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur Kettenregel.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es ist hilfreich wenn ihr bereits Exponentialfunktionen und die Kettenregel kennt. Falls nicht könnt ihr dies gerne noch nachlesen.

E-Funktion ableiten

Klären wir zunächst warum die E-Funktion so besonders ist.

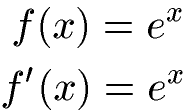
In den meisten Fällen liegt jedoch nicht einfach nur e hoch x vor, sondern es sind Funktionen bzw. Gleichungen, die etwas anspruchsvoller sind. Daher sehen wir uns nun die Ableitung von Funktionen an, bei denen "e" mit beteiligt ist.

Beispiel 1: Kettenregel für E-Funktion

Wie lautet die erste Ableitung dieser E-Funktion?

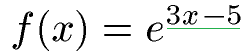
Lösung:

E-Funktionen werden mit der Kettenregel abgeleitet. Um diese anzuwenden muss man nach innerer und äußerer Funktion unterteilen. Die innere Funktion ist der Exponent mit 3x - 5. Wir leiten diesen mit der Potenzregel ab und erhalten v'(x) = 3. Die äußere Funktion ist e hoch irgendetwas, abgekürzt mit e^v. Die Ableitung von e hoch irgendetwas oder kurz e^v bleibt e hoch irgendwas oder kurz e^v. Innere und äußere Ableitung werden miteinander multipliziert und für v setzen wir wie am Anfang festgelegt wieder 3x - 5 ein.

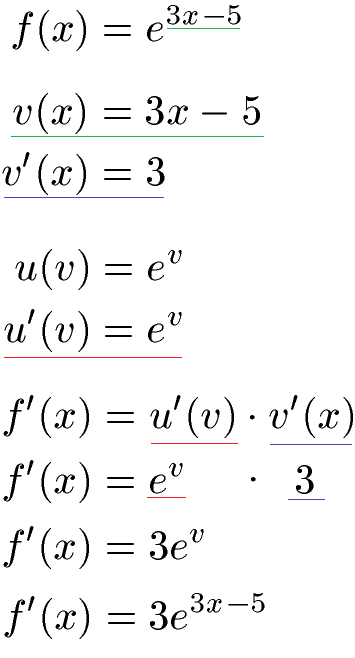
Anzeige:

E-Funktion: Produktregel und Kettenregel

Sehen wir uns ein komplizierteres Beispiel an, bei welchem für die Ableitung die Produktregel und die Kettenregel gebraucht wird.

Beispiel 2: Produktregel und Kettenregel

Wie lautet die erste Ableitung der folgenden Funktion?

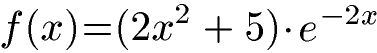
Lösung:

Steht es nicht in der Aufgabenstellung muss man zunächst verstehen welche Ableitungsregeln benötigt werden. Wirft man einen Blick auf die Gleichung sieht man innerhalb der Klammer eine Potenz. Am Ende gibt es eine E-Funktion mit -2x im Exponenten, was auf eine Kette hindeutet. Die Gleichung ist aus zwei Funktionen zusammengesetzt, welche jeweils ein x beinhalten. Daher haben wir ein Produkt.

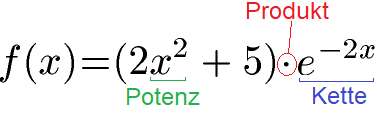
Für die erste Ableitung benutzen wir zunächst die Produktregel. Wir unterteilen dazu die Gleichung in u = 2x² + 5 und v = e^-2x. Die Ableitung von 2x² + 5 lässt sich mit der Potenzregel zu u' = 4x einfach ermitteln. Etwas schwieriger wird es mit der E-Funktion. Hier gilt:

• Erste Ableitung = Innere Ableitung mal äußere Ableitung

Um die Kettenregel anzuwenden zu können leiten wir den Exponenten ab. Für die innere Ableitung der Funktion wird aus -2x die innere Ableitung -2. Die äußere Ableitung der Funktion bleibt erhalten, bleibt damit e^-2x. Multiplizieren wir -2 mit e^-2x erhalten wir die Ableitung v' = -2e^-2x. Für u, u', v und v' setzen wir alles in den allgemeinen Zusammenhang für die Produktregel ein und erhalten dadurch die Ableitung.

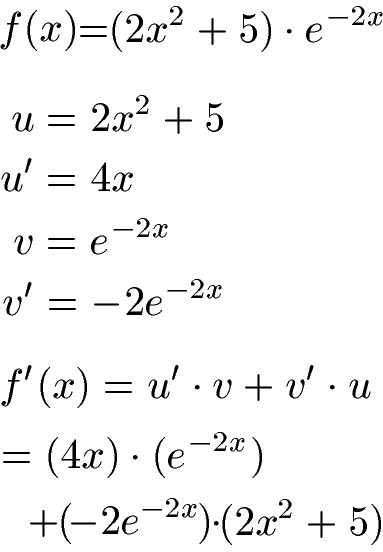
Aufgaben / Übungen E-Funktion ableiten

Aufgabe 1:

Fangen wir etwas einfacher an:

• Wie lautet die Ableitung von f(x) = e^x?

• f'(x) = e^x
• f'(x) = xe^x
• f'(x) = e^ex
• f'(x) = e¹

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Kettenregel

Fragen mit Antworten E-Funktion Ableitung