Symmetrie / Symmetrieverhalten einer Funktion

Mit der Symmetrie bzw. dem Symmetrieverhalten von Funktionen befassen wir uns hier. Dies sehen wir uns an:

• Eine Erklärung, welche Symmetriearten es gibt.
• Beispiele für Symmetrieverhalten.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur Symmetrie von Funktionen.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es ist hilfreich wenn ihr bereits wisst wie man eine Funktion zeichnet.

Erklärung Symmetrie

In der Mathematik untersucht man verschiedene Arten von Symmetrie. Wer bereits weiß was er/sie sucht kann gleich zum entsprechenden Thema springen. Wer dies noch nicht weiß findet im Anschluss eine Einleitung in das jeweilige Thema.

Typische Symmetrieuntersuchungen:

• Spiegelsymmetrie / Achsensymmetrie
• Punktsymmetrie zum Ursprung
• Punktsymmetrie zu beliebigem Punkt

Spiegelsymmetrie / Achsensymmetrie

Die erste Art von Symmetrie für die man sich in der Mathematik interessiert ist die Spiegelsymmetrie, auch Achsensymmetrie genannt. Genauer gesagt untersucht man dabei meistens die Symmetrie zur y-Achse. Die nächste Grafik zeigt die Funktion y = x². Die Funktion wurde in blau eingezeichnet. Wie man recht einfach sehen kann ist es möglich jeden Punkt dieser Parabel an der y-Achse (rot) zu spiegeln und man landet auf der anderen Seite wieder auf dem Funktionsverlauf.

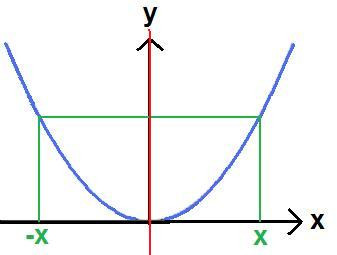
Wie man so etwas rechnen kann und weitere Erklärungen dazu findet ihr unter:

• Spiegelsymmetrie / Achsensymmetrie

Anzeige:

Beispiel Symmetrieverhalten

Sehen wir uns zwei weitere Beispiele zum Symmetrieverhalten an. Dies wären die Punktsymmetrie zum Ursprung und die Punktsymmetrie zu einem beliebigem Punkt.

Symmetrieverhalten zum Ursprung

Um die Punktsymmetrie zum Ursprung zu verstehen zeichnen wir erneut ein x-y-Koordinatensystem und markieren mit einem roten Punkt den Schnittpunkt der Achsen. Bei der Symmetrie zum Ursprung kann man jeden Punkt der blauen Funktion an dem Ursprung spiegeln und landet auf der anderen Seite ebenfalls wieder auf dem blauen Funktionsgraphen.

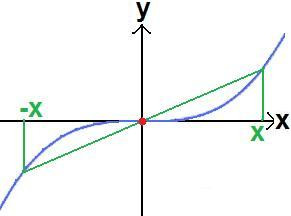
Wie man dies rechnet und weitere Erklärungen dazu findet ihr unter:

• Punktsymmetrie zum Ursprung

Symmetrie zu beliebigem Punkt

Der Punkt an dem gespiegelt wird muss nicht wie im letzten Beispiel der Ursprung des Koordinatensystems sein. Der Punkt kann auch irgendwo liegen. Die nächste Grafik zeigt einen Funktionsverlauf bei dem man glauben könnte, dass bei x = 2 eine Punktsymmetrie vorliegen könnte.

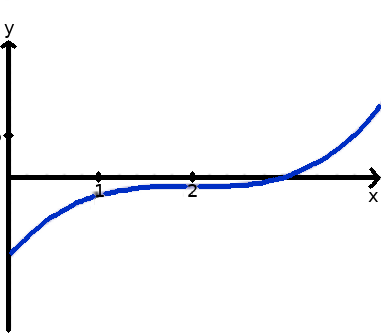
Wie man dies überprüfen kann findet ihr ausführlich vorgestellt unter:

• Punktsymmetrie zu beliebigem Punkt

Video Symmetrie

Anzeigen:

Fragen mit Antworten Symmetrieverhalten