Quotientenregel Ableitung

Die Quotientenregel für Ableitungen lernt ihr hier. Dies sehen wir uns an:

• Eine Erklärung, was die Quotientenregel ist.
• Beispiele wie man diese Ableitungsregel anwendet.
• Aufgaben / Übungen um das Thema selbst zu üben.
• Ein Video zur Quotientenregel.
• Ein Frage- und Antwortbereich zu diesem Gebiet.

Tipp: Es gibt unterschiedliche Ableitungsregeln um Funktionen oder Gleichungen abzuleiten. Bevor ihr euch die Quotientenregel hier anseht, solltet ihr die Grundlagen der Ableitung kennen sowie die Potenzregel.

Quotientenregel Erklärung

Es gibt verschiedene Regeln in der Mathematik um Funktionen abzuleiten. Eine dieser Ableitungsregeln ist die Quotientenregel.

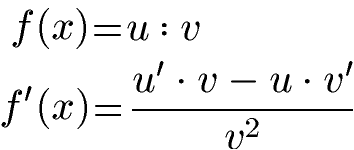
Beispiel 1: Quotientenregel anwenden

Wie lautet die 1. Ableitung des folgendes Bruchs? Eine Vereinfachung ist nicht nötig.

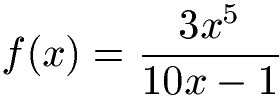
Lösung:

Wir unterteilen den Quotienten in Zähler und Nenner. Dabei setzen wir den Zähler u = 3x⁵ und den Nenner v = 10x - 1. Mit der Potenzregel leiten wir beides ab. Dabei erhalten wir für die Ableitung vom Zähler u' = 3 · 5x⁴. Im Nenner bleibt bei der Ableitung nur die 10 übrig. Im Anschluss setzen wir die allgemeine Gleichung für die Ableitung ein. Beachtet dabei die farbigen Unterstreichungen.

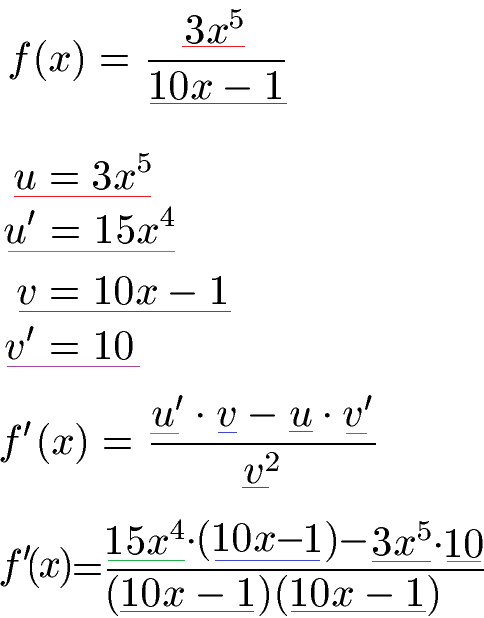
Anzeige:

Quotientenregel 2. Ableitung und Kettenregel

In diesem Abschnitt gibt es zwei weitere Beispiele. Im zweiten Beispiel wird zusätzlich noch die Kettenregel benötigt. Im dritten Beispiel soll die Quotientenregel zwei Mal eingesetzt werden um die 2. Ableitung zu berechnen.

Beispiel 2: Quotientenregel und Kettenregel

Wie lautet die erste Ableitung der nächsten Funktion? Vereinfache im Anschluss.

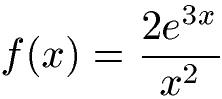
Lösung:

Auch in diesem Beispiel unterteilen wir nach Zähler und Nenner. Dabei setzen wir u = 2e^3x und v = x². Die x² sind mit der Potenzregel recht einfach abzuleiten und bringen uns v' = 2x. Bei 2e^3x muss die Kettenregel für die Ableitung eingesetzt werden. Der Faktor 2 vorne bleibt erhalten. Im Anschluss muss innere mal äußere Ableitung für die Kettenregel berechnet werden. Der Exponent 3x abgeleitet ergibt einfach 3 und e^3x bleibt erhalten. Danach setzen wir alle vier Angaben in die allgemeine Quotientenformel ein.

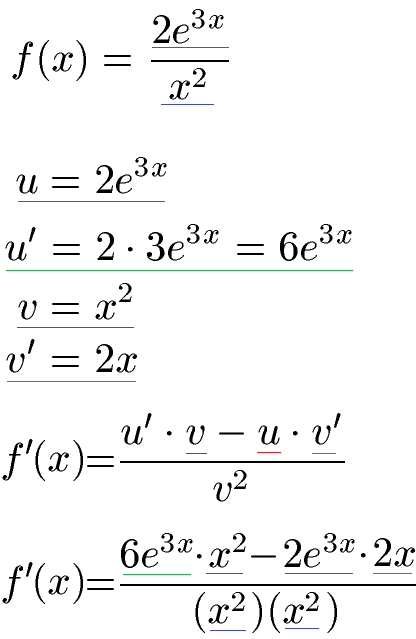
Fehlt uns noch die Vereinfachung der ersten Ableitung. Während der Zähler einfach zusammen zu fassen ist, muss man beim Nenner aufpassen. Hier muss bei der Multiplikation von x² · x² beachtet werden, dass die beiden Exponenten addiert werden. Wir erhalten als neuen Exponenten 2 + 2 = 4. Im Anschluss kürzen wir x in Zäher und Nenner. Als letzten Schritt Klammern wir 2e^3x aus.

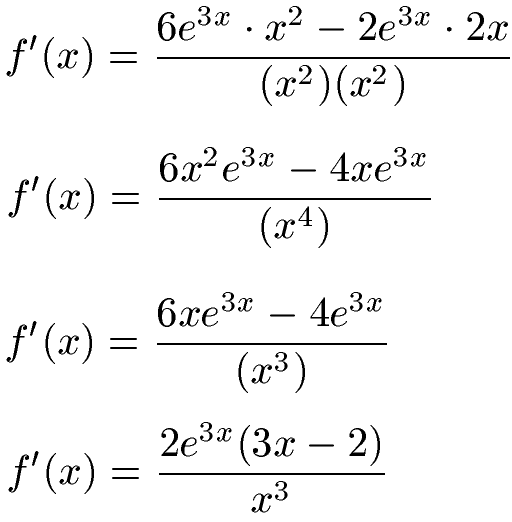
Beispiel 3: Quotientenregel 2. Ableitung

Dies soll mit der nächsten Funktion gemacht werden:

• Die 1. Ableitung bestimmen.
• Die 1. Ableitung vereinfachen.
• Den letzten Bruch der 1. Ableitung raus suchen.
• Mit diesem Bruch die 2. Ableitung berechnen.

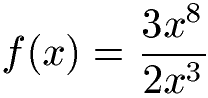
Lösung:

Wir verwenden zunächst die Quotientenregel um die erste Ableitung zu berechnen. Dazu setzen wir den Zähler u = 3x⁸ und den Nenner v = 2x³. Mit der Potenzregel bilden wir jeweils die Ableitung. Dabei reduziert sich jeweils der Exponent um 1. Der ursprüngliche Exponent wird jeweils mit dem Faktor davor multipliziert. In die allgemeine Formel der Quotientenregel werden alle Angaben eingesetzt (Siehe farbige Unterstreichungen). Im Anschluss vereinfachen wir Zähler und Nenner und kürzen.

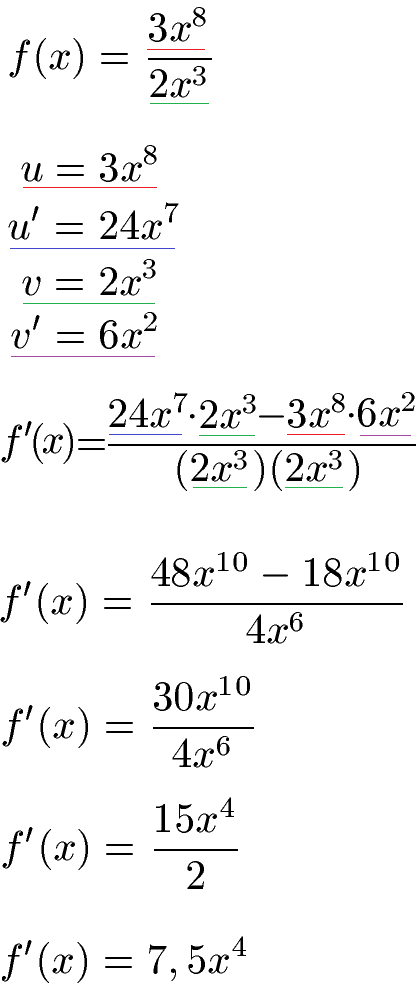
Hinweis: Es soll die 2. Ableitung mit der Quotientenregel berechnet werden. Selbstverständlich kann f'(x) = 7,5x⁴ auch mit der Potenzregel abgeleitet werden.

Kommen wir zur 2. Ableitung mit der Quotientenregel. Dazu nehmen wir die letzte Variante der ersten Ableitung mit f'(x) = 15x⁴ : 2. Wir setzen u = 15x⁴ und v = 2. Beides leiten wir mit der Potenzregel ab und vereinfachen im Anschluss.

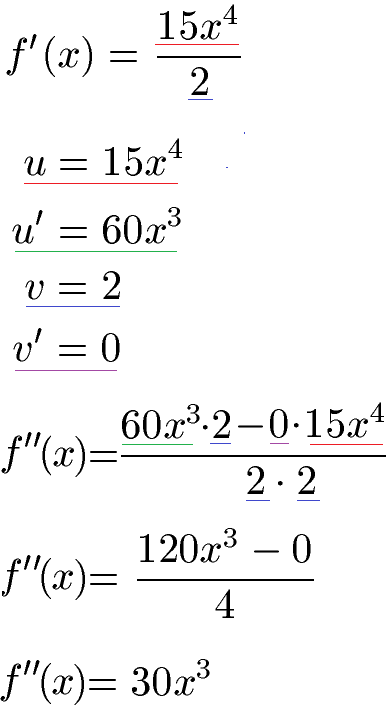
Aufgaben / Übungen Quotientenregel

Aufgabe 1:

Starten wir mit einer Frage bevor ihr Funktionen / Gleichungen ableiten sollt:

• Wann setzt man die Quotientenregel ein?

• Ableitung Differenz
• Ableitung Summe
• Ableitung Bruch
• Ableitung Produkt

Weiter zur Lösung » Aufgabe überspringen »

Du hast 0 von 3 Aufgaben erfolgreich gelöst.

Anzeigen:

Video Quotientenregel

Fragen mit Antworten Quotientenregel